La libreria scikit-fem è molto interessante in ambito matematico e scientifico, si presta alla risoluzione di equazioni differenziali tramite metodi agli elementi finiti. Quindi una gestione più avanzata di quanto abbiamo visto ad esempio con il metodo FTCS, "differenze finite" - equazione della diffusione.
Anche per chi non ne conosce i dettagli matematici, almeno a livello di rappresentazione ha già visto risultati di simulazioni tramite FEM (appunto, Finite Element Method), come la trasmissione delle tensioni, sforzo-deformazione di un oggetto, ecc. Fondamentale infatti dal punto di vista della progettazione ingegneristica di oggi, in tutti gli ambiti.
Della libreria scikit-fem ne vediamo solo un' "assaggio", con delle immagini di esempio e il relativo codice.
Come installare scikit-fem:
tramite pip: pip install scikit-fem[all]; l'opzione [all] è consigliata per poter fare uso delle dipendenze opzionali, altrimenti prendendo dei template, pezzi di codice già scritti, potrebbe essere richiesto in seguito di installare le dipendenze necessarie una ad una.
In alternativa tramite git, si può anche installare da GitHub: git clone https://github.com/kinnala/scikit-fem e poi all'interno della directory, seguire la procedura di installazione (README.md, verificare le dipendenze requirements.txt).
Secondo quanto dichiarato dal sito ufficiale, scikit-fem ha queste caratteristiche (alcune delle quali ho già avuto modo di testare):
- minime dipendenze richieste (altre librerie)
- non contiene codice compilato
- supporta elementi finiti e mesh di tipo 1D, triangolari, quadrangolari (2D), tetraedriche, esaedriche (3D)
- incude elementi e metodi più avanzati, come funzioni di Raviart-Thomas, Nédélec, MINI, Crouzeix-Raviart, Argyris, ...
Dalla documentazione di scikit-fem, vediamo Gallery of Examples, dalla quale riportiamo questi interessanti casi di esempio, poi mostrato nell'immagine finale:
- Example 21: Structural Vibration: ecco il relativo codice:
from skfem import *
from skfem.models.elasticity import linear_elasticity,\
lame_parameters
import numpy as np
from pathlib import Path
m = MeshTet.load(Path(__file__).parent / 'meshes' / 'beams.msh')
e1 = ElementTetP2()
e = ElementVector(e1)
ib = Basis(m, e)
K = asm(linear_elasticity(*lame_parameters(200.0e9, 0.3)), ib)
rho = 8050.0
@BilinearForm
def mass(u, v, w):
from skfem.helpers import dot
return dot(rho * u, v)
M = asm(mass, ib)
L, x = solve(
*condense(K, M, D=ib.get_dofs("fixed")), solver=solver_eigen_scipy_sym()
)
if __name__ == "__main__":
from skfem.visuals.matplotlib import draw, show
sf = 10.0
m.translated(sf * x[ib.nodal_dofs, 0]).draw().show()
- Example 22: Adaptive Poisson equation: ecco il relativo codice:
from skfem import *
from skfem.models.poisson import laplace
from skfem.helpers import grad
import numpy as np
m = MeshTri.init_lshaped().refined(2)
e = ElementTriP1()
def load_func(x, y):
return 1.
@LinearForm
def load(v, w):
x, y = w.x
return load_func(x, y) * v
def eval_estimator(m, u):
# interior residual
basis = Basis(m, e)
@Functional
def interior_residual(w):
h = w.h
x, y = w.x
return h ** 2 * load_func(x, y) ** 2
eta_K = interior_residual.elemental(basis, w=basis.interpolate(u))
# facet jump
fbasis = [InteriorFacetBasis(m, e, side=i) for i in [0, 1]]
w = {'u' + str(i + 1): fbasis[i].interpolate(u) for i in [0, 1]}
@Functional
def edge_jump(w):
h = w.h
n = w.n
dw1 = grad(w['u1'])
dw2 = grad(w['u2'])
return h * ((dw1[0] - dw2[0]) * n[0] +
(dw1[1] - dw2[1]) * n[1]) ** 2
eta_E = edge_jump.elemental(fbasis[0], **w)
tmp = np.zeros(m.facets.shape[1])
np.add.at(tmp, fbasis[0].find, eta_E)
eta_E = np.sum(.5 * tmp[m.t2f], axis=0)
return eta_K + eta_E
if __name__ == "__main__":
from skfem.visuals.matplotlib import draw
draw(m)
for itr in reversed(range(6)):
basis = Basis(m, e)
K = asm(laplace, basis)
f = asm(load, basis)
I = m.interior_nodes()
u = solve(*condense(K, f, I=I))
if itr > 0:
m = m.refined(adaptive_theta(eval_estimator(m, u))).smoothed()
def visualize():
from skfem.visuals.matplotlib import draw, plot
ax = draw(m)
return plot(m, u, ax=ax, shading='gouraud', colorbar=True)
if __name__ == "__main__":
visualize().show()
Vediamo infine una rappresentazione di questi due esempi e di alcune immagini generali della tanto nota Analisi agli Elementi Finiti.
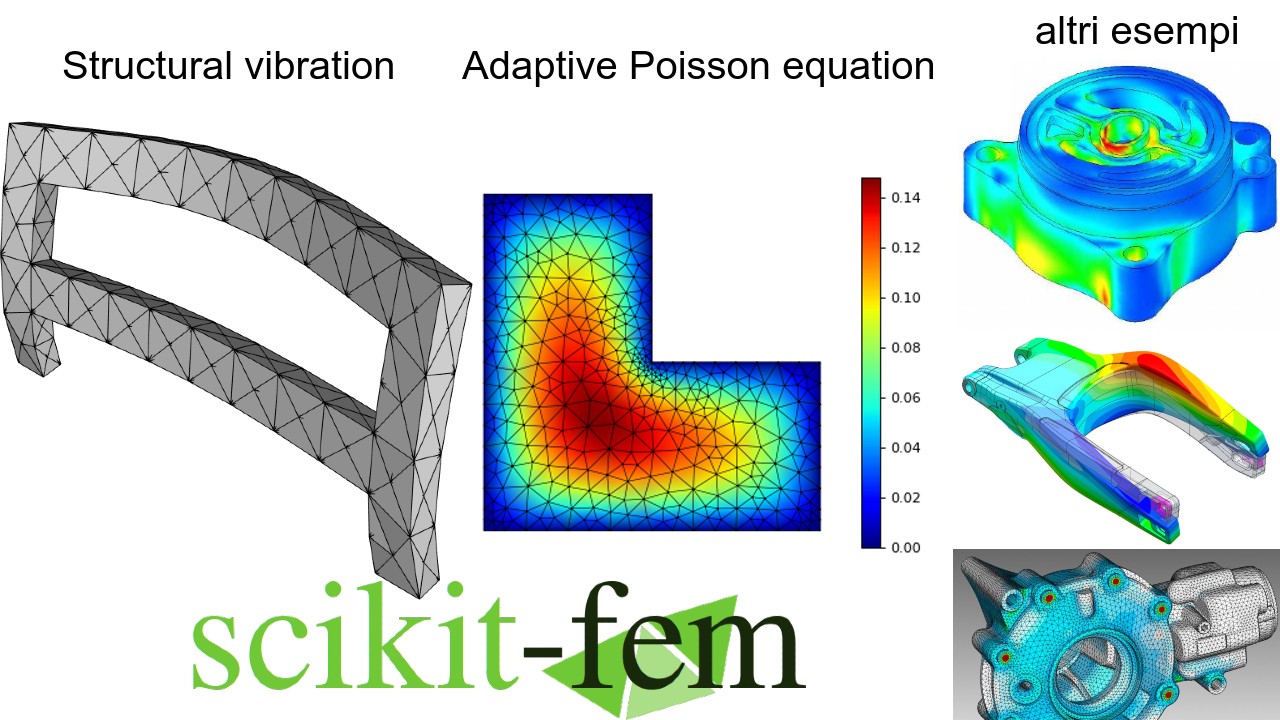
Osservazione: come detto, scikit-fem può risultare una libreria estremamente utile in ambito ingegneristico, dove trovare dei template, codice già predisposto con algoritmi di questo genere, è piuttosto comodo, rispetto a doverlo scrivere tutto da zero. Ricordiamo un unico dettaglio, algoritmi di questo tipo (elementi finiti, differenze finite, ecc) in genere se applicati ad un dominio esteso e con elevata ricchezza di dettaglio, ciò significa un grande numero di calcoli e, siccome Python non è il linguaggio più consono lato efficienza, come ben sappiamo, le possibilità fondamentalmente diventano:
- scrivere tutto in un linguaggio come C, che gestisce l'elaborazione e i risultati (es. matrice) vengono semplicemente acquisiti dal programma in Python, per rappresentarli graficamente, come avevamo fatto in questo esempio: Unire C e Python nel modo migliore
- Eseguire codice C in Python tramite CFFI ovvero, manteniamo di per sé la struttura del programma interamente in Python, ma le singole operazioni "onerose" vengono implementate da una funzione in linguaggio C e poi, seguendo la procedura alla discussione linkata, Python fa uso della memoria condivisa e di conseguenza una volta gestita questa complessità, l'efficienza totale risulta praticamente uguale a quella di un programma scritto in C, vale a dire anche potenzialmente oltre 60 volte più veloce (vedi benchmark di esempio fra vari linguaggi)