La libreria Matplotlib di Python è molto interessante e ricca di funzionalità.
Tutti i dettagli sul sito ufficiale matplotlib.org.
Viene usato principalmente per mostrare a video grafici di funzioni matematiche, quindi un interessante strumento per chi programma con Python e vuole vedere un risultato grafico. Ricca di funzionalità, estremamente versatile, Matplotlib è davvero una scelta molto interessante.
Per installare Matplotlib, la strada da seguire in un sistema Linux Debian-based (come accennavo nella discussione riguardo alla libreria Qiskit di Python):
pip install matplotlib
Ovviamente nel caso non fosse installato pip, procedere prima con uno dei comandi seguenti:
sudo apt install pip
sudo apt install python3-pip
sudo apt install python-pip
Per le distribuzioni Arch-based:
sudo pacman -S python-pip
Matplotlib lavora bene in cooperazione con l'altra libreria di Python molto usata in ambito scientifico, Numpy. Per installarla, semplicemente:
pip install numpy
Fatta questa premessa su Matplotlib, vediamo un caso pratico (richiede una matematica un pochino avanzata, tipico caso di ingegneria): equazione della diffusione 1D, risolta numericamente tramite schema FTCS alle differenze finite. Riportiamo i dati del problema:
- N=100 (numero celle)
- BCl: la cella di sinistra ha permeabilità nulla, valore costante zero
- BCr: analogo a BCl per la cella di destra, valore costante zero
- H(X): condizioni iniziali valore zero ovunque, tranne nella seconda cella ovvero C[1] dato che come indice si parte da C[0] e il valore è C[1]=100
- passo di discretizzazione: delta=0.25, il limite massimo per la stabilità tramite Von Neumann Analysis per FTCS 1D è 0.5
- Tout=1000*dt: equivale a dire, tempo finale 1000 iterazioni
Dunque la situazione iniziale, con 100 celle, è di questo tipo:
0 | 100 | 0 | ... 0
Dopo un certo numero di iterazioni (in questo caso, 1000) l'andamento diffusivo mostrerà un risultato differente, ovviamente nel tempo il picco C=100 tende ad attenuarsi mentre nelle zone vicine il valore inizialmente zero, tende a crescere. Si ha appunto un fenomeno diffusivo.
Nella seguente immagine, screenshot da Linux Mint con Python 3.10.4, vediamo il codice Python del programma, output a video nel terminale e grafico realizzato tramite Matplotlib.
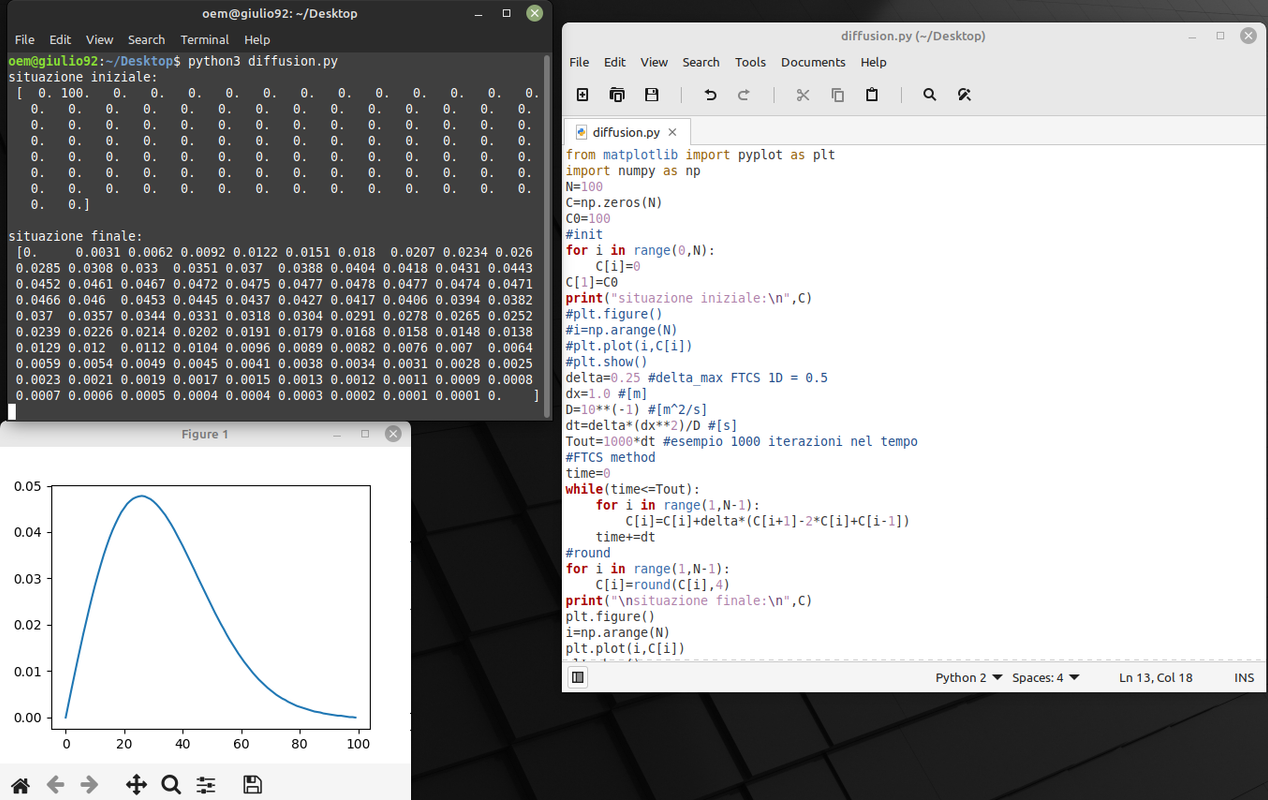
Infine, anche il codice sorgente dell'esempio in questione:
from matplotlib import pyplot as plt
import numpy as np
N=100
C=np.zeros(N)
C0=100
#init
for i in range(0,N):
C[i]=0
C[1]=C0
print("situazione iniziale:\n",C)
#plt.figure()
#i=np.arange(N)
#plt.plot(i,C[i])
#plt.show()
delta=0.25 #delta_max FTCS 1D = 0.5
dx=1.0 #[m]
D=10**(-1) #[m^2/s]
dt=delta*(dx**2)/D #[s]
Tout=1000*dt #esempio 1000 iterazioni nel tempo
#FTCS method
time=0
while(time<=Tout):
for i in range(1,N-1):
C[i]=C[i]+delta*(C[i+1]-2*C[i]+C[i-1])
time+=dt
#round
for i in range(1,N-1):
C[i]=round(C[i],4)
print("\nsituazione finale:\n",C)
plt.figure()
i=np.arange(N)
plt.plot(i,C[i])
plt.show()