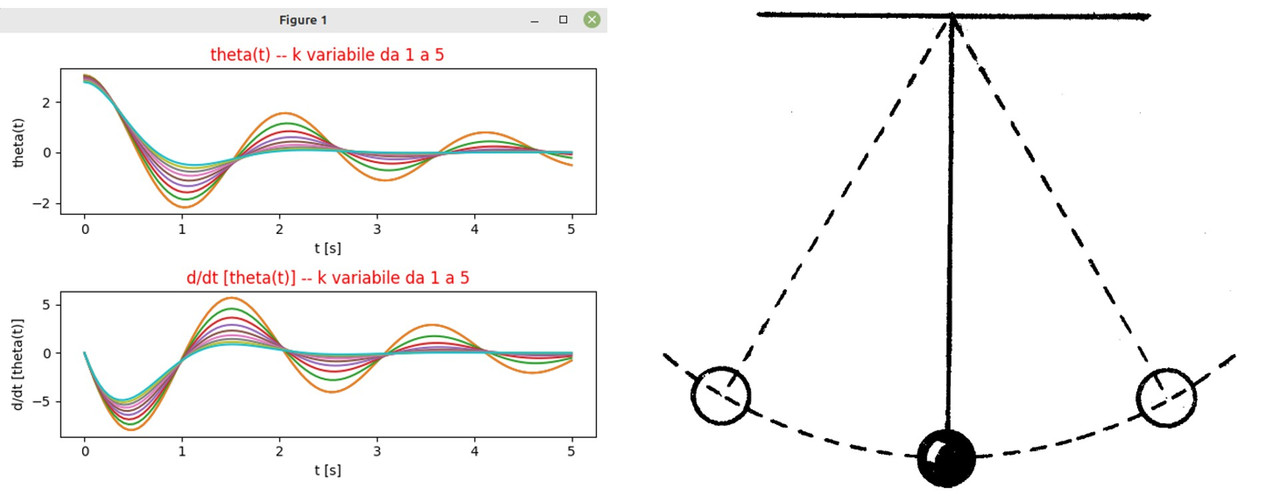
Abbiamo già illustrato qualche esempio con la libreria Matplotlib di Python; anche per quanto riguarda l'ambito ingegneristico, ad esempio studio deformazione trave, equazione diffusione - metodo numerico FTCS, idrodinamica - correnti fluviali 1D. Vediamo ora un caso che mi è capitato alla mano, si tratta di un vecchio esercizio di ingegneria (questo esercizio faceva parte di un esame opzionale, corso a scelta che attribuiva un solo credito in totale). Vediamo quindi lo studio dell'oscillazione del pendolo con attrito, con l'ipotesi di non conservazione dell'energia (l'attrito tende a smorzare le oscillazioni).
Di seguito si riporta il codice:
import numpy as np
from matplotlib import pyplot as plt
g=9.81
theta0=np.pi/8.0
EPS=10**(-6)
m=1
l=1
k=1
t=np.linspace(0,5,100) #dominio del tempo
fig,ax=plt.subplots(2,1) #2 grafici
def pendolo(t,m,l,theta0):
w=np.sqrt(g/l-(0.5*k/m))
tau=w*m/k
phi=np.arctan(-1/(w*tau))
A=w/(np.cos(phi)+EPS)
theta=A*np.exp(-t/tau)*np.cos(w*t+phi)
return theta
def dp(t):
return (pendolo(t+EPS,m,l,theta0)-pendolo(t,m,l,theta0))/EPS
i=1
while i<5:
ax[0].plot(t,pendolo(t,m,l,theta0))
ax[1].plot(t,dp(t))
k=i
i+=(5-1)/10.0
ax[0].set_title("theta(t) -- k variabile da 1 a 5",color="red")
ax[1].set_title("d/dt [theta(t)] -- k variabile da 1 a 5",color="red")
ax[0].set_xlabel("t [s]")
ax[0].set_ylabel("theta(t)")
ax[1].set_xlabel("t [s]")
ax[1].set_ylabel("d/dt [theta(t)]")
plt.tight_layout() #ottimizza gli spazi
plt.show()
Per quanto riguarda l'andamento grafico, vediamo in alto l'oscillazione indicata con theta(t) ovvero funzione del tempo; il grafico sotto la sua derivata nel tempo. A destra una schematizzazione del pendolo, quindi concettualmente le oscillazioni si smorzano nel tempo a causa dell'attrito (come avviene infatti nella realtà). Le diverse linee nei grafici indicano diversi valori della costante "k", che comportano smorzamento più o meno accentuato.