Dopo aver parlato dell'ottima libreria Python Matplotlib, con un esempio di risoluzione numerica dell'equazione di diffusione tramite metodo FTCS, vediamo un altro caso (fatto con Linux Mint, Python 3.10.4), che poi suddiviso in due sottocasi: studiamo il comportamento idrodinamico di una corrente a pelo libero, un fiume in modo uniforme, per chi ha conoscenze di idrodinamica riconosce bene le convenzioni e sa di cosa parlo.
Brevemente, Yu è l'altezza del fiume in moto uniforme, Yc è un valore di altezza critica, siamo inizialmente nel caso Yu>Yc (nel caso Yu<Yc, cambia il comportamento, si passa per un caso limite Yu=Yc, stato critico, che poi evidenziamo nel caso 2).
- caso 1: moto uniforme 1D, dati assegnati, risoluzione nel caso generale per convergenza, implementando una variante del metodo della bisezione (fissiamo il numero di iterazioni anziché controllo sull'errore). Ecco il codice:
import numpy as np
#moto uniforme 1D
#Q=UY=bYks(bY(b+2y))^(2/3)
#caso generale: f(Y)=0
Q=100
b=100
ks=25
iff=0.005
g=9.8
def f(Y):
return Q-b*Y*ks*(iff**0.5)*((b*Y)/(b+2*Y))**(2/3)
#bisezione con N iterazioni
def bisez(a,b,N):
for i in range(0,N):
c=0.5*(a+b)
if(f(a)*f(b)<0):
if(f(a)*f(c)<0):
b=c
else:
a=c
return a
#Yc=(Q^2/(gb^2))^(1/3)
Yc=(Q**2/(g*b**2))**(1/3)
print("situazione iniziale:\n")
print("Yu=",bisez(0,3,10))
print("Yc=",Yc)
- caso 2: per semplicità facciamo l'ipotesi b>>y, comunque verificata (100 > 0,7 circa), quindi si semplifica la procedura; l'obiettivo qui è un altro, ovvero aumentare la pendenza del fondo affinché si abbia variazione di Yu, dato che Yc rimane costante; vogliamo vedere l'andamento di Yu, quando interseca (equivale a) Yc. Ecco il codice:
import numpy as np
from matplotlib import pyplot as plt
#moto uniforme 1D
#Q=UY=bYks(if^0.5)(bY(b+2y))^(2/3)
#ipotesi b>>y: Y=(Q/(ksb(if^0.5)))^(3/5)
Q=100 #portata
b=100 #larghezza
ks=25 #scabrezza del fondo
iff=0.005 #pendenza
g=9.8 #accelerazione gravità
Y=(Q/(b*ks*iff**0.5))**0.6
Yc=(Q**2/(g*b**2))**(1/3)
print("situazione iniziale:\n")
print("Yu=",Y)
print("Yc=",Yc)
print("\naumentiamo la pendenza del fondo:\n")
N=50
V=np.zeros(N)
Ycc=np.zeros(N)+Yc
for i in range(0,N):
V[i]=(Q/(b*ks*(iff+0.001*i)**0.5))**(3/5)
print(V)
plt.figure()
i=np.arange(N)
plt.xlabel((iff+0.001*i)*100)
plt.plot(i,V[i],Ycc[i])
plt.show()
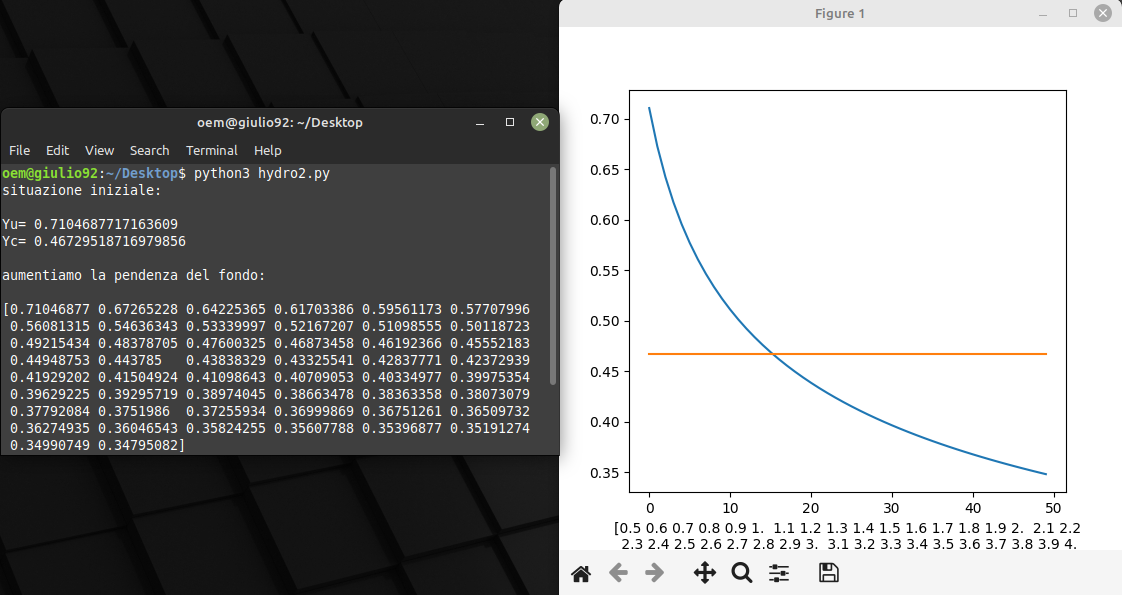
Infine un'immagine per questo secondo caso, in arancio è Yc, costante; in blu Yu, che varia (diminuisce) aumentando la pendenza del fondo, mantenendo costante la relazione Q=U*A ovvero se la corrente più veloce, il livello è più basso (a parità di condizioni), e viceversa. In ascissa il numero di iterazioni (50), sotto un array che indica la pendenza espressa in % (0.5 = 0.5%), in ordinata il livello dell'acqua, in metri.