Dopo aver visto studio deformazione trave e idrodinamica - correnti fluviali 1D con Python Matplotlib, vediamo ora un interessante caso di ingegneria!
Come dimensionare una tubazione idraulica con il metodo delle tensioni ammissibili
Il metodo delle tensioni ammissibili è una procedura abbastanza rapida per quanto riguarda la progettazione: un metodo che combina geometria e caratteristiche del materiale, per dare origine ad un valore di tensione di progetto, che va verificata con la tensione massima ammissibile. Quindi per chi progetta, interviene sulle variabili che può controllare (in questo caso specifico, potrebbe essere sia il diametro della tubazione che la pressione massima) affinché sia soddisfatta la verifica.
I nostri dati di esempio sono:
- tratto di tubazione lungo 10 metri
- materiale acciaio strutturale S275, tensione massima ammissibile 275 MPa
- tubazione con diametro esterno 10cm, diametro interno 8cm
- schema statico a doppio incastro, carico uniformemente distribuito che (trascurando il peso proprio) è determinato dalla pressione del fluido
Vediamo come procedere:
- dal teorema di Bernoulli, troviamo l'equivalenza fra il termine di pressione (Pa=N*m, eventualmente convertiamo in atm per nostra comodità) e la portata (m3/s)
- spinta dinamica: trascurando la componente di spinta statica, abbiamo S=densità*portata2/area, densità dell'acqua 1000 kg/m3
- risolviamo il semplice schema statico, ottenendo momento massimo pari a Mmax=(qL2)/8 al centro (quindi dove c'è maggiore sollecitazione)
- S=[N], q=[N/L] quindi sostituiamo per ottenere q=S/L
- Mmax=tensione*modulo_resistenza (Wx), dove Wx=3.14(Dmax4-Dmin4)/(32Dmax)
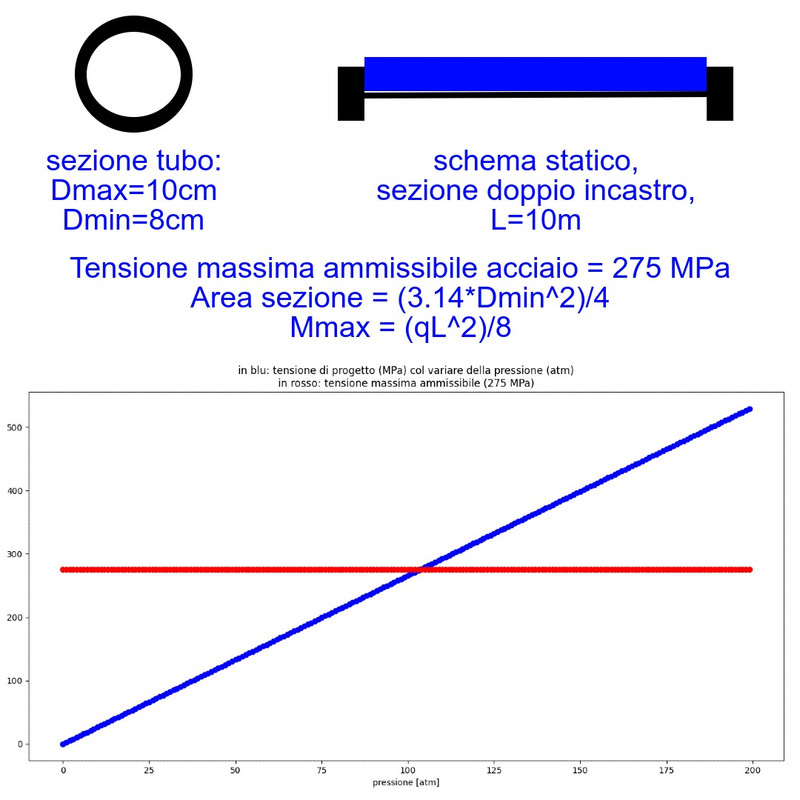
Con questi dati di progetto, il programma in Python considera una pressione nel tubo che parte da zero fino a 200 atmosfere, per vedere il risultato in termini di tensione equivalente sulla struttura, tubazione. Il punto di equilibrio come si può vedere circa P=100atm. Vale a dire che per una pressione inferiore, la verifica è soddisfatta, per una pressione superiore invece struttura e materiale non sono sufficienti. Ovviamente nella pratica si deve prendere anche un certo margine di sicurezza aggiuntivo!
Questo è il codice Python, con molti dei passaggi illustrati prima a parole, già semplificati per il risultato finale, per "snellire" il codice :
import numpy as np
from matplotlib import pyplot as plt
Dmax=0.1 #m
Dmin=0.08 #m
L=10 #m
sigma_max=275 #Mpa
plt.figure()
for Pj in range(0,200): #pressione, da zero a 200atm
plt.plot(Pj,(1e-6)*(2.0*Pj*101325*Dmin**2*L**2*Dmax**2)/(Dmax**3-Dmin**3),'o',color="blue")
plt.plot(Pj,sigma_max,'o',color="red")
plt.title("in blu: tensione di progetto (MPa) col variare della pressione (atm)\nin rosso: tensione massima ammissibile (275 MPa)")
plt.xlabel("pressione [atm]")
plt.show()
Infine un'immagine per rendere meglio l'idea: in alto la sezione del tubo e lo schema statico, in basso il grafico che mostra la tensione in funzione della pressione (in blu) e in rosso la tensione massima ammissibile. Come detto, si vede il punto di incontro a circa P=100atm.