Vediamo un caso di risoluzione di equazione differenziale ordinaria (ODE) in Python, con una procedura semplice e funzionale.
scipy.integrate.solve_ivp, da docs.scipy.org, è una funzione ("Solve Initial Value Problem") che consente di risolvere un problema differenziale ai valori iniziali in modo robusto e scalabile; a seconda del contesto, applica il metodo numerico più opportuno, fra cui:
- RK45 (Runge-Kutta-Fehlberg 4(5)): un metodo esplicito avanzato che calcola simultaneamente una soluzione di ordine 4 e una di ordine 5 (più precisa) e in base alla differenza fra le due soluzioni (stima errore locale) viene adattata la dimensione del passo di integrazione)
- RK23 (Runge-Kutta-Fehlberg 2(3)): simile al precedente, usa la coppia di ordine 2 e 3, meno preciso ma più performante se non abbiamo richiesta di elevata accuratezza
- metodi impliciti: Radau, BDF (Backward Differentiation Formula), vedi anche BTCS, ideale per problemi rigidi, "stiff"
- altro: ad esempio LSODA (Livermore Solver for Ordinary Differential Equations), solver "swich" ovvero un metodo adattivo che stima il problema e passa da un metodo numerico all'altro cercando di rilevare in automatico la scelta più funzionale
- caso di studio: esempio decadimento radioattivo, si tratta di una ODE semplice del tipo
dy/dt=-ky, la cui soluzione analitica è facilmente calcolabile, pari a y(t) = y0 * e-kt; vogliamo applicare la soluzione numerica di default di scipy.integrate.solve_ivp e vedere graficamente il risultato
Ecco il codice Python3 di questo problema.
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
def f(t, y, k): # funzione modello decadimento radioattivo
dydt = -k * y
return dydt
k = 0.5 # Costante di decadimento
y0 = [20] # Stato iniziale (deve essere un array/lista)
t_span = [0, 10] # Simula da t=0 a t=10
t_eval = np.linspace(t_span[0], t_span[1], 100) # Punti in cui vogliamo la soluzione
# 'args' è una tupla usata per passare i parametri extra (k) alla funzione del modello
sol = solve_ivp(f, t_span, y0, args=(k,), t_eval=t_eval)
tempo = sol.t
valori_y = sol.y[0] # sol.y è 2D, prendiamo la prima (e unica) riga
plt.plot(tempo, valori_y,'o',color="red") #soluzione numerica
plt.plot(tempo,y0[0]*np.exp(-k*tempo),color="blue") #soluzione analitica
plt.title('Simulazione del Decadimento Esponenziale')
plt.xlabel('Tempo')
plt.ylabel('Quantità')
plt.grid(True)
plt.show()
Ecco l'immagine di come appare il grafico, poi lo commentiamo.
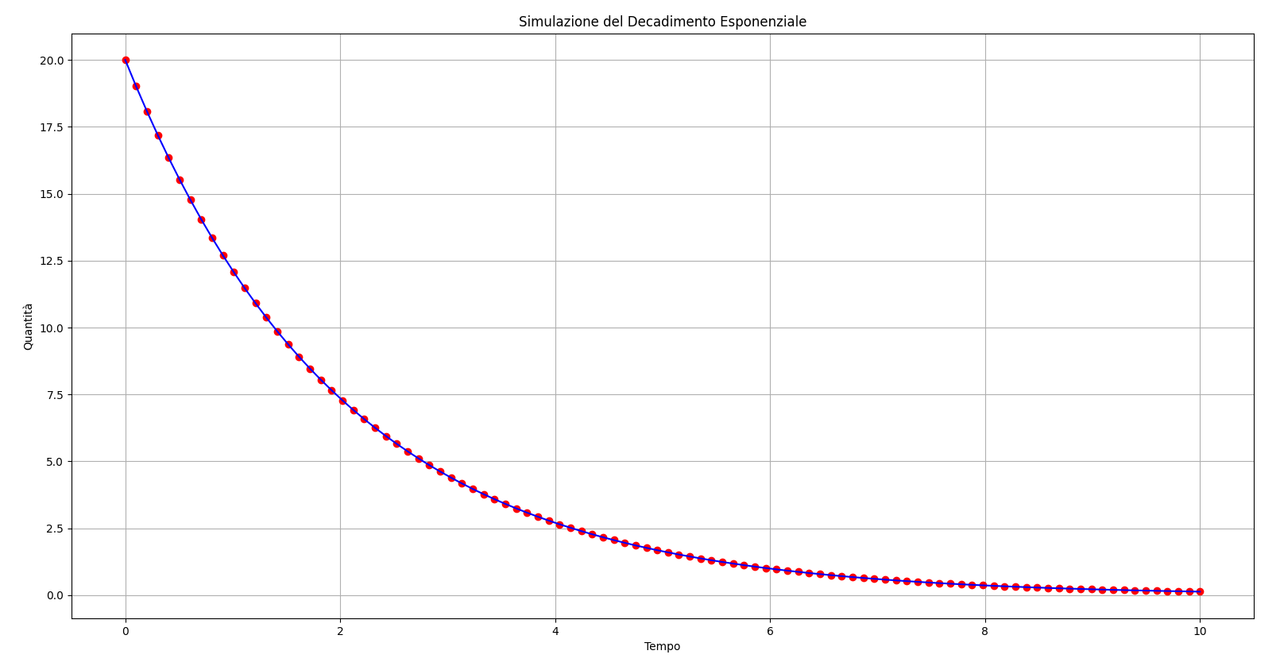
Ovviamente i dati usati sono indicativi. La linea continua è la soluzione analitica mentre i puntini indicano la soluzione numerica. Rispetto all'implementazione ad-hoc di un metodo numerico (es. come fatto nell'esempio modello preda-predatore Lotka-Volterra), applicare un metodo risolutivo già predisposto, strutturato e robusto come questo che è lo strumento standard in Python per risolvere ODE, integrato nella libreria SciPy, è conveniente se non abbiamo particolare necessità di scelta specifica.
Un'interessante estensione al problema può essere l'applicazione manuale dell'estrapolazione di Richardson, a cui sarà opportuno dedicare una discussione a parte: ovvero solve_ivp non usa direttamente questo metodo numerico, ma possiamo applicare noi la combinazione lineare di soluzioni numeriche con passi di discretizzazione diversi col fine di minimizzare l'errore complessivo, come appunto la filosofia dell'estrapolazione di Richardson, questo anche lavorando con la funzione già integrata solve_ivp (analogamente a come invece potremmo fare partendo da un metodo numerico predefinito).
Una precisazione, riguardo alle performance: in questo caso la richiesta computazionale era semplice, caso di esempio con poche iterazioni del metodo numerico. Python essendo linguaggio interpretato, non è particolarmente orientato all'efficienza computazionale, come invece C/C++ (vedi Benchmark performance C, Python, MATLAB - GNU Octave, JavaScript, PHP). Tuttavia, anche per Python se volessimo introdurre delle sottigliezze di ottimizzazione, potremmo procedere in questo modo, modificando il codice:
- simulazione di molti decadimenti simultanei (quindi più risoluzioni numeriche assieme), es. 100 valori k random, in una sola chiamata vettorizzata
- broadcasting NumPy per calcolare soluzioni in parallelo (vedi calcolo parallelo)
- questo è adatto ad esempio a simulazioni Monte Carlo o problemi computazionali complessi
- eventualmente un'implementazione specifica di altri metodi numerici vettorizzati, senza solve_ivp, migliorerebbe ancora le performance (da notare che in questo caso, risolvibile tranquillamente anche per via analitica, la soluzione numerica è stata scelta come semplice esempio di applicazione per mostrare il funzionamento di solve_ivp)
Ecco quindi il codice aggiornato con le ottimizzazioni discusse e commenti al codice (essendoci in questo caso più simulazioni random, i risultati e il grafico saranno differenti ad ogni esecuzione).
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
def f(t, y, k): # y è ora vettore (forma: n_variabili x n_simulazioni)
return -k[:, np.newaxis] * y # Broadcasting: k (1D) moltiplica y (2D)
n_sim = 100 # Numero di simulazioni parallele
k = np.random.uniform(0.1, 1.0, n_sim) # Array di k diversi
y0 = np.full((1, n_sim), 20.0) # y0 vettorializzato: 1 variabile x n_sim
t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 100)
# Solve_ivp vettorializzato: risolve tutto in parallelo
sol = solve_ivp(f, t_span, y0.flatten(), args=(k,), t_eval=t_eval, vectorized=True, method='RK45')
# vectorized=True abilita la modalità vettoriale interna di solve_ivp
# y0.flatten() per compatibilità, ma sol.y sarà reshaped
# Reshape: forma (1*n_sim, n_t) -> (1, n_sim, n_t)
valori_y = sol.y.reshape(1, n_sim, -1)
tempo = sol.t
# Soluzione analitica vettorializzata (broadcasting NumPy)
y_analitica = y0[:, :, np.newaxis] * np.exp(-k[:, np.newaxis, np.newaxis] * tempo[np.newaxis, np.newaxis, :])
# Plot solo la media per semplicità (o plotta tutte)
plt.plot(tempo, valori_y[0].mean(axis=0), 'o', color="red", label='Numerica (media)')
plt.plot(tempo, y_analitica[0].mean(axis=0), color="blue", label='Analitica (media)')
plt.title('Simulazione Vettorializzata (Media di 100 Decadimenti)')
plt.xlabel('Tempo')
plt.ylabel('Quantità')
plt.grid(True)
plt.legend()
plt.show()