Dopo aver visto il caso FTCS - equazione diffusione - Python Matplotlib, vediamo un caso analogo ma più complesso, ovvero il metodo numerico BTCS applicato all'equazione della diffusione.
Nota: l'equazione della diffusione, dal punto di vista matematico presenta la stessa forma sia che si tratti di temperatura, concentrazione di una sostanza, ecc, i dati numerici e il significato fisico che diamo, dipendono dal singolo contesto di applicazione.
Rispetto al metodo FTCS, BTCS è in forma implicita e quindi richiede un algoritmo iterativo per la risoluzione del sistema (ad esempio, metodo della bisezione). In questo caso, è stata scelta una strada più efficiente dato che, ad esempio, il classico metodo dell'eliminazione di Gauss ha complessità O(N3), mentre, trattandosi di un sistema tridiagonale (ovvero una matrice piena di zeri, tranne su tre diagonali, la principale e quelle sotto e sopra di essa), possiamo usare l'algoritmo di Thomas che presenta complessità O(N) quindi estremamente più efficiente all'aumentare della dimensione della matrice!
Il codice è stato scritto in Python, per rappresentarlo direttamente tramite la libreria Matplotlib. In questo caso, il numero di operazioni non era molto elevato, altrimenti sarebbe stato più efficiente risolverlo ad esempio in C e rappreentare con Python solamente l'output grafico.
import numpy as np
import matplotlib.pyplot as plt
# Parametri
L = 1.0 # Lunghezza dominio spaziale
T = 0.1 # Tempo finale
D = 0.1 # Coefficiente di diffusione
N = 100 # Numero di punti nello spazio
M = 1000 # Numero di passi temporali
dx = L / N
dt = T / M
alpha = D * dt / dx**2
# Condizioni iniziali e di bordo
u0 = np.zeros(N)
u0[int(N / 2)] = 1.0 # Impulso iniziale al centro
BC_left = 0.0 # Condizione di bordo sinistra (u(0, t) = BC_left)
BC_right = 0.0 # Condizione di bordo destra (u(L, t) = BC_right)
# Costruzione della matrice tridiagonale per l'algoritmo di Thomas
a = -alpha * np.ones(N-1)
b = (1 + 2 * alpha) * np.ones(N)
c = -alpha * np.ones(N-1)
# Applichiamo le condizioni al contorno
b[0] += alpha
b[-1] += alpha
# Array per memorizzare la soluzione
u = np.zeros((M+1, N))
u[0] = u0
# Algoritmo di Thomas per ogni passo temporale
for i in range(1, M+1):
d = u[i-1].copy()
# Applicazione delle condizioni al contorno
d[0] += alpha * BC_left
d[-1] += alpha * BC_right
# Risoluzione del sistema tridiagonale
for j in range(1, N):
w = a[j-1] / b[j-1]
b[j] -= w * c[j-1]
d[j] -= w * d[j-1]
u[i][-1] = d[-1] / b[-1]
for j in range(N-2, -1, -1):
u[i][j] = (d[j] - c[j] * u[i][j+1]) / b[j]
# Plot della soluzione all'ultimo istante di tempo
plt.figure(figsize=(8, 6))
plt.plot(np.linspace(0, L, N), u[0], color='blue')
plt.plot(np.linspace(0, L, N), u[5], color='red')
plt.plot(np.linspace(0, L, N), u[10], color='green')
plt.title('Andamento gaussiano alla fine del tempo')
plt.xlabel('Spazio')
plt.ylabel('Temperatura')
plt.ylim([0, 1.1]) # Imposta il limite dell'asse y per rendere visibile l'andamento gaussiano
plt.grid(True)
plt.show()
Nota: in "Array per memorizzare la soluzione", vediamo in questo caso che l'array è bidimensionale, quindi facciamo questa precisazione:
- bidimensionale significa che restano in memoria i valori ad ogni tempo (se sono memorizzati, poi li possiamo rivedere in un momento successivo); in termini di memoria, se gli step temporali sono 1000, significa occupare 1000 volte la dimensione della matrice (o dei vettori) originale!
- monodimensionale, quindi sovrascrivendo ogni volta la matrice/vettori; al termine, non abbiamo memorizzato in memoria i valori intermedi, come memoria occupata è sicuramente molto più leggero, dipende quindi da quale sia l'obiettivo
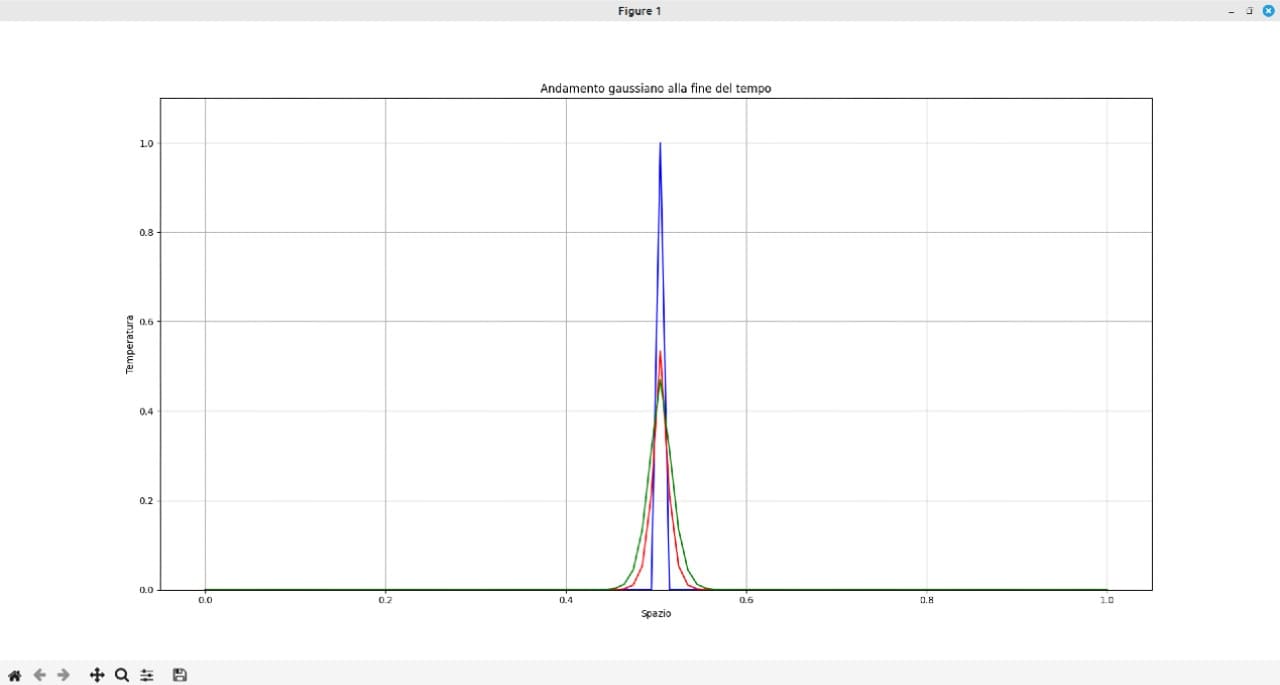
Vediamo infine l'andamento grafico del dominio nel tempo, è chiaro l'andamento diffusivo: la curva blu è in prossimità di t=0, quindi il dominio nell'istante iniziale, poi la curva rossa e successivamente quella verde. Si vede l'andamento diffusivo, attenuazione del picco al centro, che va invece ad interessare zone più estese del dominio.