Dopo aver visto un esercizio di ingegneria, studio oscillazione pendolo con attrito (risolto con Python - Matplotlib), vediamo ora un altro caso interessante (un altro esercizio del corso di ingegneria che attribuiva solamente un credito 😄)! Studio del modello preda-predatore (equazioni di Lotka-Volterra)
Questo modello fa uso delle equazioni differenziali di Lotka Volterra, ovvero in termini generali:

Questo modello matematico viene detto "preda-predatore" in quanto all'aumentare di una specie diminuisce quella antagonista e viceversa. Pensando all'equivalente del mondo reale, occorre quindi che la popolazione rimanga entro un certo range affinché possa continuare nel tempo.
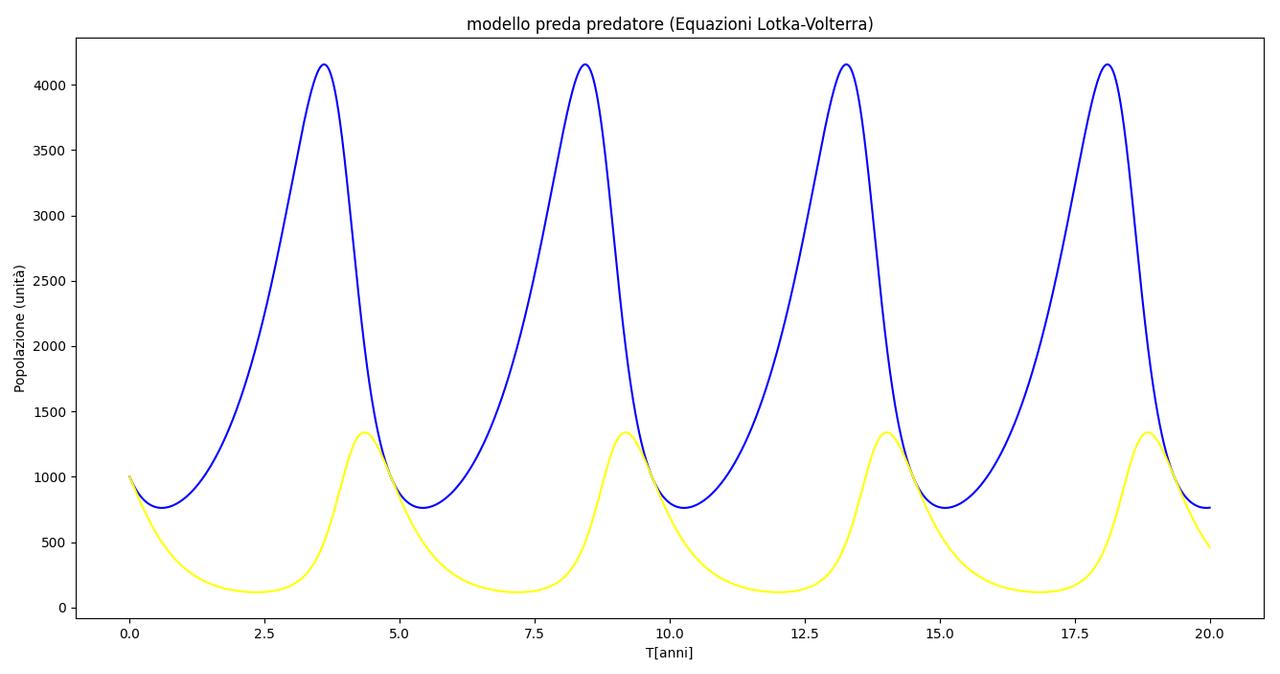
Nello specifico, come esempio preda-predatore sono stati considerati "leone e gazzella". La popolazione di partenza è stata presa con N=1000 per entrambi. Per "complicare le cose" la risoluzione del sistema di equazioni differenziali è stata effettuata per via numerica con Runge Kutta del secondo ordine.
Di seguito riportato il codice Python:
import numpy as np
from matplotlib import pyplot as plt
N=1000 #popolazione iniziale
def RungeKutta(F, U0, T, N): #metodo numerico
dt=T/N
t=np.linspace(0,T,N+1)
U=np.zeros((N+1, np.size(U0)))
U[0,:]=U0
for n in range(N):
k1=F(t[n], U[n])
k2=F(t[n+1], U[n]+dt*k1)
U[n+1]=U[n]+dt*(k1+k2)/2
return t, U
def LotkaVolterra(t,U):
A=1
B=2e-3
C=1e-3
D=2
Gazz=U[0]
Leo=U[1]
dGazzdt=(A-B*Leo)*Gazz #equazione1
dLeodt=(C*Gazz-D)*Leo #equazione2
dUdt=np.array([dGazzdt, dLeodt])
return dUdt #ritorna l'equazione
U0=np.array([1000,1000])
T=20 #anni
time, sol = RungeKutta(LotkaVolterra, U0, T, N=5000)
Gazz=sol[:,0]
Leo=sol[:,1]
plt.figure()
plt.title("modello preda predatore (Equazioni Lotka-Volterra)")
plt.plot(time, Gazz, color="blue")
plt.plot(time, Leo, color="yellow")
plt.xlabel("T[anni]")
plt.ylabel("Popolazione (unità)")
plt.show()
Questo è l'andamento grafico: in blu sono rappresentate le prede (gazzelle), in giallo i predatori (leoni). Come periodo temporale, un'estensione di 20 anni (si nota la periodicità, andamento ciclico).