Dopo aver trattato alcuni problemi di ingegneria come Dimensionamento tubazione idraulica con tensioni ammissibili e Dimensionamento reattore digestione anaerobica, vediamo un altro caso interessante: dimensionamento della camera di combustione (forno) di un inceneritore, termovalorizzatore.
Uno schema dell'impianto, ad esempio relativo al termovalorizzatore di Bolzano, lo troviamo su eco-center.it:

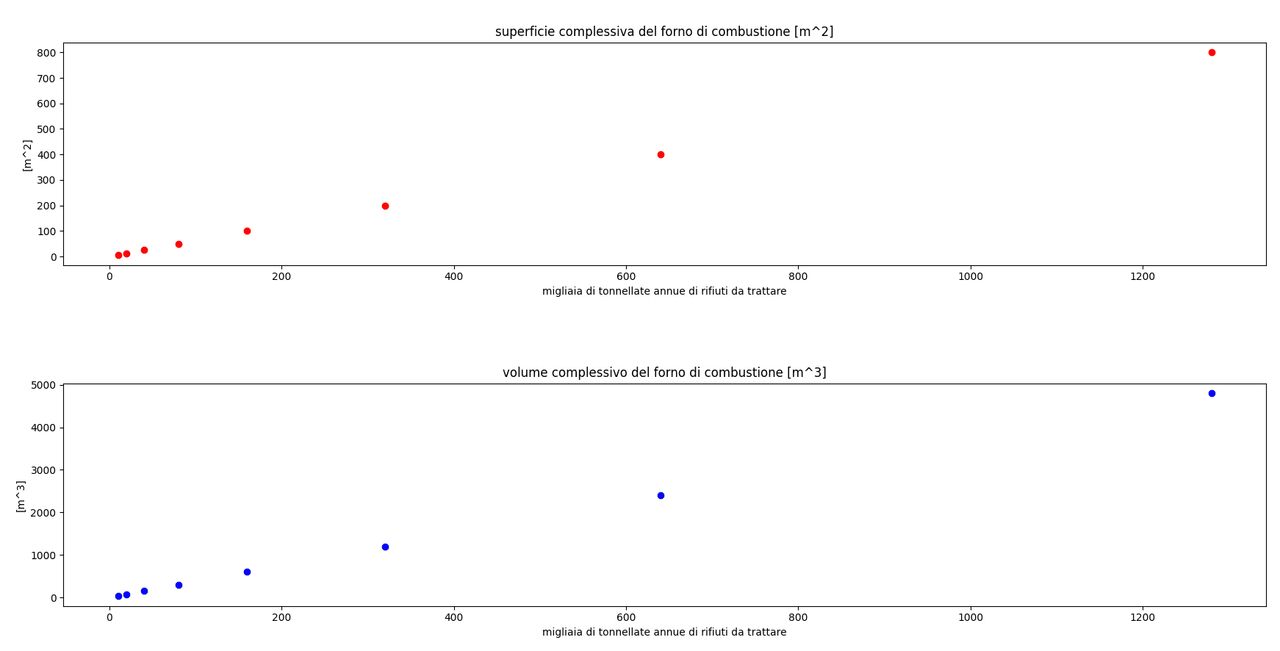
Si riporta un codice Python che partendo da alcuni dati di progetto, mostra un grafico della variazione della superficie totale e del volume totali richiesti dal forno (per funzionare con quel determinato carico termico).
In particolare è possibile modificare i valori, per vedere come cambiano i risultati: ad esempio il potere calorifico dei rifiuti (PCIu) viene considerato pari a 3000 kcal/kg (12,55 MJ/kg); da Wikipedia - potere calorifico possiamo confrontare ad esempio vari materiali, il legno di conifera arriva anche a 20 MJ/kg, gas metano 50 MJ/kg, alcol etilico 27 MJ/kg, ecc.
Nel caso in esame, il grafico mostra i valori della superficie e volume della camera di combustione (NB è il valore totale, se poi a livello di progettazione si fanno due o tre linee in parallelo, semplicemente per ogni forno di combustione si divide il totale per il numero di linee), partendo da 10.000 tonnellate annue di rifiuti da bruciare fino a 1.280.000 (ad esempio per confronto, l'impianto di Bolzano riesce a trattare 130.000 t/anno, quello di Brescia 700.000 t/anno, in Cina a Shenzhen ce n'è uno in costruzione da oltre 2 milioni di t/anno).
Il coodice è ben commentato in modo tale da poter cambiare i dati a piacere, per vedere come varia il risultato.
from matplotlib import pyplot as plt
import numpy as np
Qt = 6*10**5 #carico termico superficiale della griglia [kcal/m^2h]
Iv = 10**5 #intensità volumetrica di combustione [kcal/m^3h]
PCIu = 3000 #potere calorifico medio dei rifiuti da trattare [kcal/kg]
ore_anno = 8000 #funzionamento della griglia (quindi una media di 22 ore al giorno considerando periodi di possibile manutenzione)
tonnellate_anno=np.zeros(8) #rifiuti da trattare
Qh=np.zeros(8) #[t/h]
kcal_ora=np.zeros(8) #[kcal/h]
S=np.zeros(8)
V=np.zeros(8)
fig,ax=plt.subplots(2,1) #2 grafici
for i in range(8):
#tonnellate_anno[i]=100000*(i+1) #100.000 % 1.000.000 t/anno
tonnellate_anno[i]=10000*2**(i)
Qh[i] = tonnellate_anno[i]/ore_anno
kcal_ora[i] = Qh[i] * PCIu * 1000 # [kcal/h]
S[i] = kcal_ora[i] / Qt #[m^2]
V[i] = kcal_ora[i] / Iv #[m^3]
ax[0].plot(10*2**(i),S[i],'o',color="red")
ax[1].plot(10*2**(i),V[i],'o',color="blue")
ax[0].set_title("superficie complessiva del forno di combustione [m^2]")
ax[1].set_title("volume complessivo del forno di combustione [m^3]")
ax[0].set_xlabel("migliaia di tonnellate annue di rifiuti da trattare")
ax[1].set_xlabel("migliaia di tonnellate annue di rifiuti da trattare")
ax[0].set_ylabel("[m^2]")
ax[1].set_ylabel("[m^3]")
plt.tight_layout() #ottimizza gli spazi
plt.show()
Nello specifico, con questi dati abbiamo:
- 10.000 t/anno: S=6,25 m2, V=37,5 m3
- 20.000 t/anno: S=12,5 m2, V=75 m3
- 40.000 t/anno: S=25 m2, V=150 m3
- 80.000 t/anno: S=50 m2, V=300 m3
- 160.000 t/anno: S=100 m2, V=600 m3
- 320.000 t/anno: S=200 m2, V=1200 m3
- 640.000 t/anno: S=400 m2, V=2400 m3
- 1.280.000 t/anno: S=800 m2, V=4800 m3