L'algoritmo di Dijkstra è stato ora dimostrato essere efficiente e anche "universalmente ottimale"
Sviluppato da Edsger Dijkstra nel 1956 e pubblicato nel 1959, l'omonimo algoritmo nel corso della storia è sempre stato uno degli algoritmi più studiati, quando si tratta di cercare il cammino minimo (minizzare la somma dei costi) in un grafo, con o senza ordinamento. Le ripercussioni pratiche ovviamente sono enormi, pensiamo in generale al trasporto, sistemi complessi come chiusure stradali, traffico, oltre alla sola distanza, lineare o vincolata, fra due punti. Come detto l'algoritmo di Dijkstra era sicuramente uno dei più noti e diffusi, mancava però uno studio approfondito che lo definisse "il migliore" in tutte le situazioni.
Di recente (18 ottobre 2024) il ricercatore Václav Rozhoň del Politecnico federale di Zurigo (ETH Zurich) ha pubblicato su arxiv.org il paper ufficiale intitolato <<Instance-Optimality in I/O-Efficient Sampling and Sequential Estimation>>, in cui fondamentalmente dimostra che una variante dell'algoritmo di Dijkstra è universalmente ottimale per il problema del percorso più breve da un singolo punto di partenza. Nello specifico, una particolare struttura dati (heap) che consente di accedere rapidamente agli elementi più recenti e questa struttura dati, combinata con l'algoritmo di Dijkstra, permette di ottenere prestazioni migliori rispetto ad altre soluzioni.
Anche se non sono sempre ben chiare le possibili applicazioni immediate del nuovo algoritmo, della nuova variante, lo sviluppo di metodi numerici e teorici è sempre un forte strumento che potrà trovare applicazione in futuro (ad esempio, l'analisi numerica e relativi metodi risolutivi, sono nati concettualmente ben prima dei computer).
Questo risultato, dimostra appunto che la variante dell'algoritmo di Dijkstra ad oggi è "universalmente ottimale", ciò non toglie possibilità che in futuro, altri algoritmi riescano a determinare ottimalità anche più forti, ideali per altri problemi applicativi.
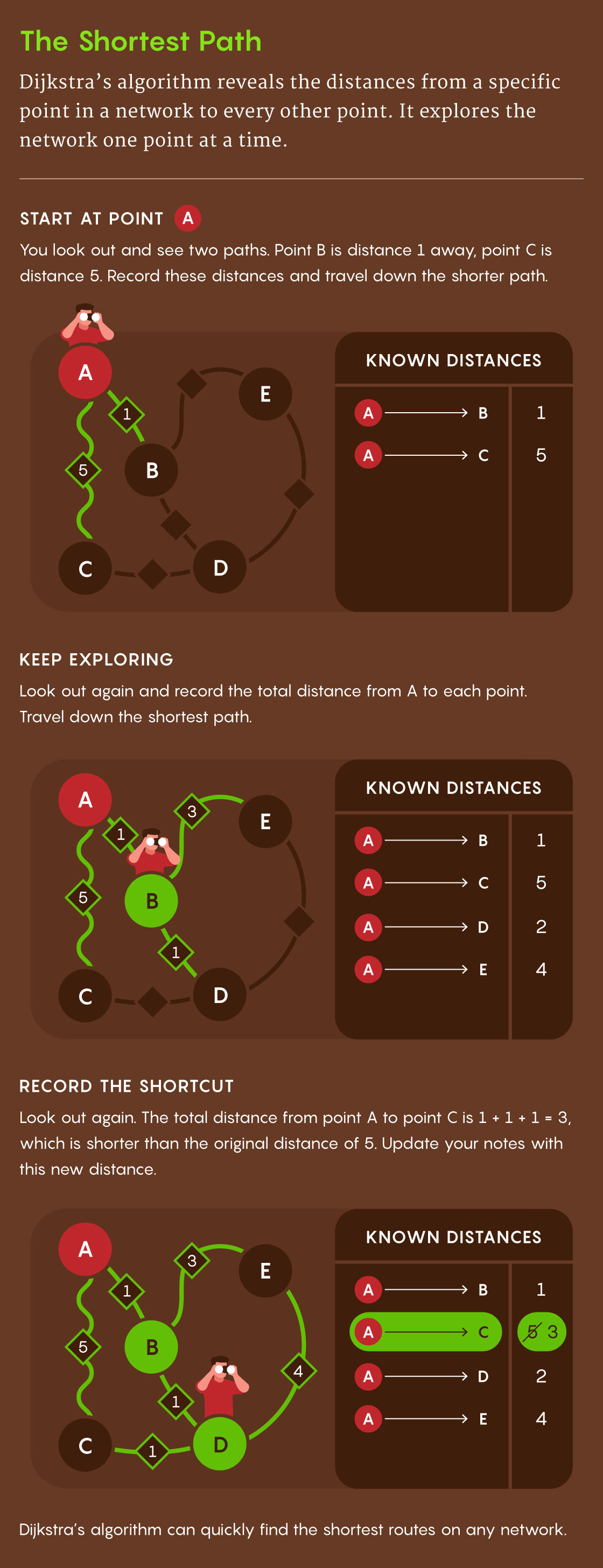
Un approfondimento in lingua inglese lo troviamo qui: quantamagazine.org. Dallo stesso sito, una raffigurazione concettuale della variante modificata dell'algoritmo di Dijkstra.