Dopo aver visto i due casi separati Python - Matplotlib - esempi grafici 3D e Python - Matplotlib: costruire una Heatmap, vediamo ora un confronto fra i due, per comprenderli meglio e vedere cosa scegliere a seconda della situazione.
Come esempio vediamo una funzione Gaussiana (media nulla, deviazione standard unitaria) nel caso z=f(x,y) ovvero nel caso spaziale, grafico 3D. In particolare, la funzione è questa: 1.0/(2*np.pi)*np.exp(-0.5*(x**2+y**2)) (sintassi tramite Python, liberia Numpy per pi greco e l'esponenziale).
Questo è il codice per il caso della rappresentazione tramite superficie 3D:*
import numpy as np
from matplotlib import pyplot as plt
N=20
def f(x,y):
return 1.0/(2*np.pi)*np.exp(-0.5*(x**2+y**2))
plt.figure()
ax = plt.axes(projection ='3d')
X,Y=np.meshgrid(np.linspace(-5, 5, N),np.linspace(-5, 5, N))
ax.plot_surface(X,Y,f(X,Y))
plt.title("Gaussiana con media 0 e std 1")
plt.show()
Questo invece il codice per la rappresentazione tramite Heatmap ("mappa di calore"); si poteva ovviamente scegliere altri colori (scala di grigi, ecc), la scelta è di esempio:
import numpy as np
from matplotlib import pyplot as plt
N=20
def f(x,y):
return 1.0/(2*np.pi)*np.exp(-0.5*(x**2+y**2))
X,Y=np.meshgrid(np.linspace(-5, 5, N),np.linspace(-5, 5, N))
color='YlGnBu'
plt.imshow(f(X,Y),color)
plt.title("Gaussiana con media 0 e std 1")
plt.show()
Infine un'immagine che mette a confronto i due grafici, in modo tale da poterli comprendere meglio.
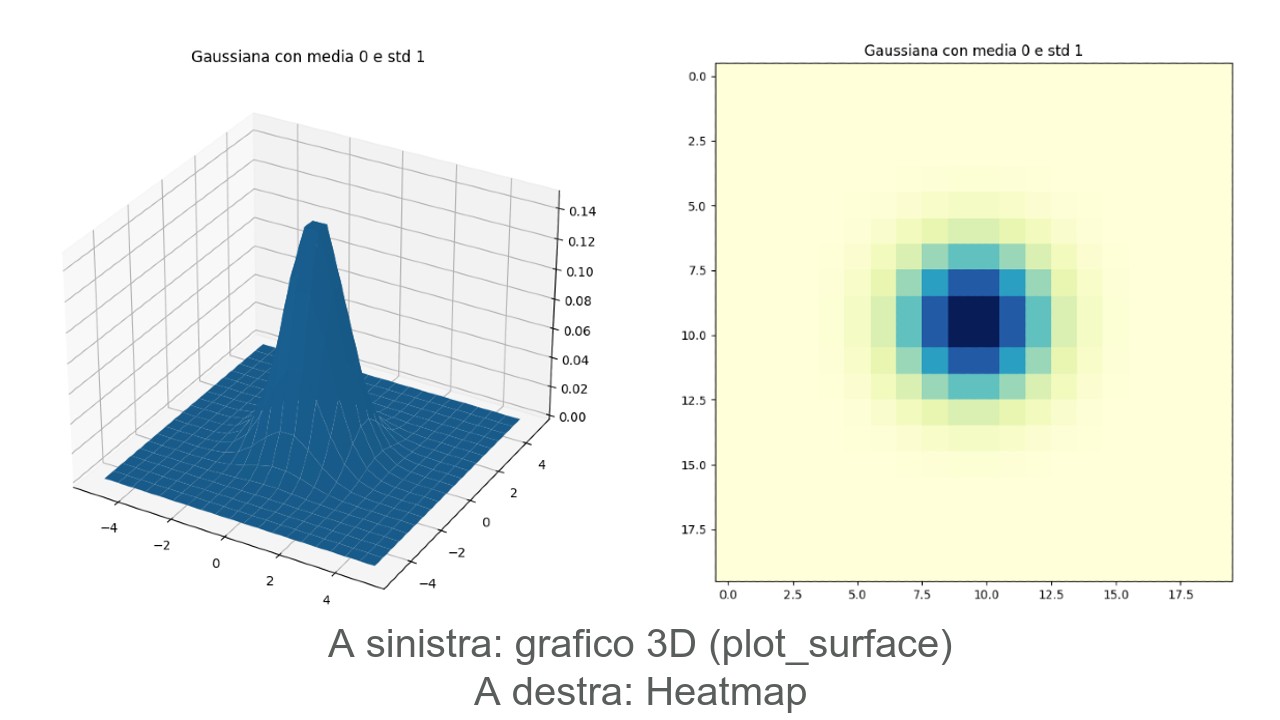
Quando conviene una superficie 3D e quando una Heatmap?
Dipende dal caso specifico, valutando la precedente immagine di confronto si può giungere alla seguente conclusione: scegliere la rappresentazione che rende più semplice la comprensione del grafico. In questo caso, una superficie 3D può andare bene, se invece il grafico inizia ad essere più complesso, difficile da visualizzare e comprendere dovendo ruotare l'immagine 3D, allora una Heatmap può rendere più chiara l'idea (è come guardarlo dall'alto ed evidenziare colori diversi a seconda della quota raggiunta ovvero f(x,y)).