Prendendo ispirazione dal celebre evento Adventofcode, in particolare il contest 12/12/2022, ho creato un problema differente (risolto poi in Python), secondo me più interessante da risolvere, visti anche i possibili risvolti pratici. Il problema definito da me è questo:
creare una matrice di dimensione Nx * Ny, contenenti valori interi random (0-1000), questi valori indicano la quota di un punto; la cella iniziale ha quota 0, la cella finale quota 1000. Dobbiamo trovare la strada più efficiente per arrivare dalla prima all'ultima cella e possiamo muoverci solo +1 in X o Y, quindi non in diagonale (per andare in diagonale occorrono insomma due spostamenti). Strada più efficiente significa meno dislivello possibile, sia in positivo che in negativo (sia fare salita che discesa, è faticoso, cerchiamo quindi un'ottimizzazione). Quindi il programma deve testare combinazioni diverse di percorso e poi mostrare il dislivello minimo.
Per praticità, essendo già parecchie righe di codice, riporto qui il caso della prima scelta di percorso (random). Il programma può essere quindi facilmente esteso in questo modo: si ripetono le stesse operazioni N volte e, se il valore "somma" è minore del precedente (vale a dire, percorso ottimizzato) allora si aggiorna tale valore, indicando quindi il nuovo percorso come migliore.
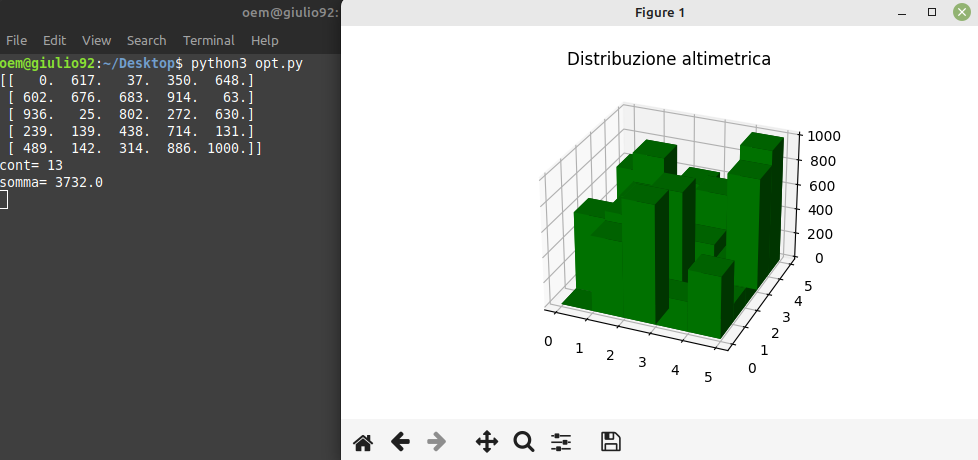
Per rendere anche visivamente più carina la cosa, riporto un grafico ad istogrammi, colorati di verde, che indicano la quota di ogni cella, quindi da intendersi come una distribuzione altimetrica!
Questo è il codice Python:
import numpy as np
import random as rd
from matplotlib import pyplot as plt
Nx=5
Ny=5
V=np.zeros((Nx,Ny))
for j in range(0,Ny):
for i in range(0,Nx):
V[i][j]=rd.randint(1,999)
V[0][0]=0
V[Nx-1][Ny-1]=1000
print(V)
posX=0
posY=0
temp=0
somma=0
cont=0
while(1):
cont+=1
temp=V[posX][posY]
k=rd.randint(0,1)
if(k==0&posX<Nx-1):
posX+=k
else:
if(posY<Ny-1):
posY+=k
if(posX>=Nx):
posX=Nx-1
if(posY>=Ny):
posY=Ny-1
if(posX==Nx-1):
posY+=1
if(posY==Ny-1):
posX+=1
somma+=((V[posX][posY]-temp)**2)**0.5
if((posX==Nx-1)&(posY==Ny-1)):
break
print("cont=",cont)
print("somma=",somma)
plt.figure()
ax = plt.axes(projection ='3d')
for j in range(Ny):
for i in range(Nx):
ax.bar3d(i, j, 0, 1, 1, V[i][j], color="green")
plt.title("Distribuzione altimetrica")
plt.show()
Qui mostrato invece l'andamento grafico: a sinistra la matrice mostrata nel terminale, a destra il grafico 3D realizzato tramite istogrammi. La variabile "cont" indica il totale di passi effettuati (un cammino lungo gli assi verticali e orizzontali della matrice), "somma" è il dislivello totale, con tutti i saliscendi.