Abbiamo già visto qualche esempio in ambito fisica tecnica, in particolare il rendimento di una macchina termica, andamento diffusione termica in coordinate radiali. Vediamo oggi il caso dell'irraggiamento termico. Qualche premessa:
L'irraggiamento è uno dei tre modi attraverso cui avviene la propagazione del calore. In particolare, al contrario della conduzione e della convezione, l'irraggiamento non prevede contatto diretto tra gli scambiatori, e non necessita di un mezzo per propagarsi
La quantità di calore emessa da un corpo per irraggiamento è infatti proporzionale a T4, cioè alla quarta potenza della sua temperatura (in gradi Kelvin)
NB: la situazione può essere ad esempio valutare la potenza termica scambiata per irraggiamento di un corpo esposto al sole, quindi temperatura ambiente e temperatura del corpo riscaldato.
In questo caso di studio, abbiamo questi elementi:
- Th = temperatura più alta
- Tl = temperatura più bassa (gradi °C, poi nella formula la convertiamo in gradi Kelvin)
- ipotesi di corpo nero (termine eps=1, altrimenti abbiamo 0<eps<1, infatti un corpo nero si scalda di più di un corpo di colore più chiaro)
- formula irraggiamento: P [Watt/m2] = sigma * eps * (Th4-Tl4), costante sigma = 5,67 * 10-8
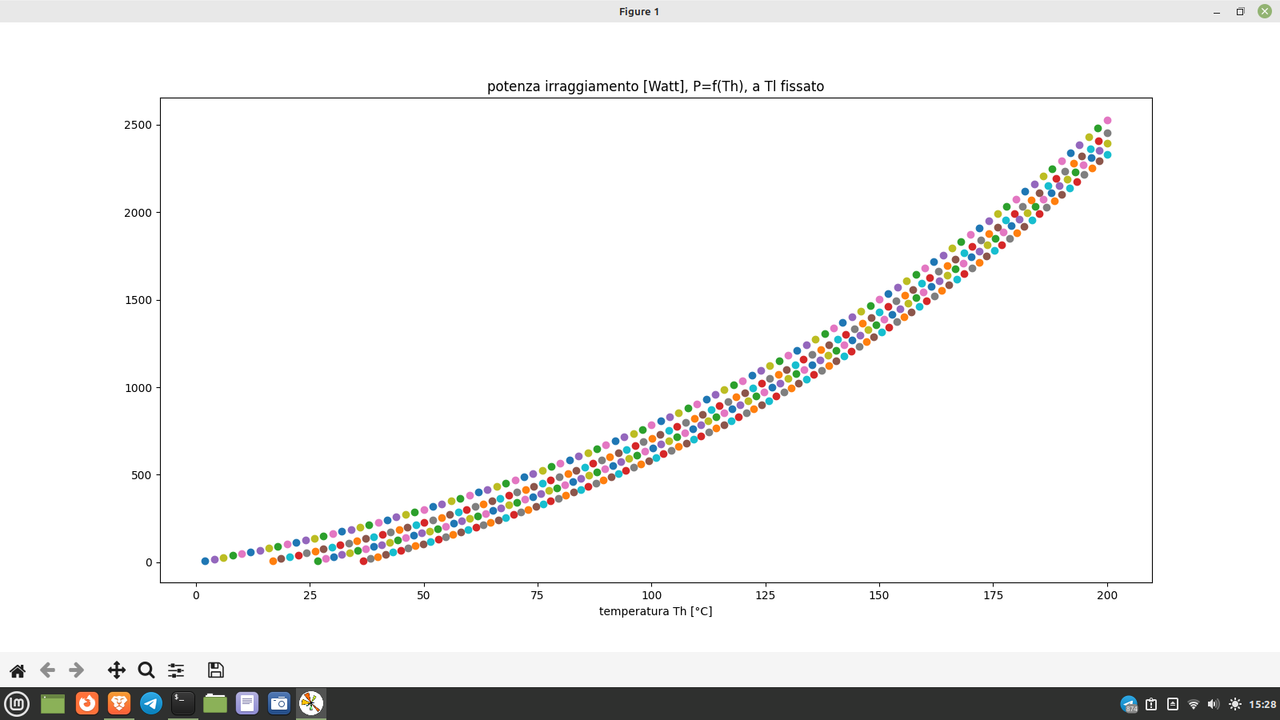
Vediamo come varia l'andamento della potenza (netta) in Watt/m2 scambiata per irraggiamento, in funzione della temperatura Th (più è alta e più ovviamente la potenza risultante è maggiore), questo per diversi valori di Tl (es. temperatura ambiente). Nell'esempio, abbiamo ottenuto quattro curve della potenza in funzione di Th, per Tl fissato ovvero:
- Tl[0] = 0 °C
- Tl[1] = 15 °C
- Tl[2] = 25 °C
- Tl[3] = 35 °C
Come risultato, abbiamo ottenuto quattro curve: quella più alta, ha Tl fissato inferiore (0 °C nell'esempio) mentre quella più bassa ha Tl fissato maggiore (35 °C nell'esempio). Questo perché fa variare il termine Th4-Tl4.
Di seguito riportato il codice Python. Se si vuole sperimentare, si possono es. cambiare i valori iniziali dell'array Tl oppure cambiare il range dei valori di Th.
import numpy as np
from matplotlib import pyplot as plt
#P=sigma*eps*(Th^4-Tl^4)
sigma=5.67*10**(-8) #costante
eps=1 #ipotesi corpo nero
Tl=[0,15,25,35] #°C
Th=np.zeros(4)
Tmax=200 #°C
#Tl+=273.15 #from °C to K
Tl[0]+=273.15
Tl[1]+=273.15
Tl[2]+=273.15
Tl[3]+=273.15
Tmax+=273.15 #from °C to K
N=100
Th[0]=Tl[0]
Th[1]=Tl[1]
Th[2]=Tl[2]
Th[3]=Tl[3]
plt.figure()
for i in range(N):
Th[0]+=(1.0/N)*(Tmax-Tl[0])
Th[1]+=(1.0/N)*(Tmax-Tl[1])
Th[2]+=(1.0/N)*(Tmax-Tl[2])
Th[3]+=(1.0/N)*(Tmax-Tl[3])
plt.plot(Th[0]-273.15,sigma*eps*(Th[0]**4-Tl[0]**4),'o') #curva Tl[0]
plt.plot(Th[1]-273.15,sigma*eps*(Th[1]**4-Tl[1]**4),'o') #curva Tl[1]
plt.plot(Th[2]-273.15,sigma*eps*(Th[2]**4-Tl[2]**4),'o') #curva Tl[2]
plt.plot(Th[3]-273.15,sigma*eps*(Th[3]**4-Tl[3]**4),'o') #curva Tl[3]
plt.title("potenza irraggiamento [Watt], P=f(Th), a Tl fissato")
plt.xlabel("temperatura Th [°C]")
plt.show()
Infine uno screenshot dell'output grafico, con le varie curve a Tl costante.