Ho analizzato un caso di studio interessante, considerata la crescita globale dell'IA, vediamo una simulazione tramite modello matematico, sistema di equazioni differenziali, poi risolto numericamente.
I presupposti del modello sono:
- U1, U2, U3 = livello di sviluppo dell'IA (lo quantifichiamo come budget investito) per USA, Europa, Cina rispettivamente; partiamo da valori iniziali e studiamo la crescita nel tempo (assumiamo dati iniziali: USA=10, Europa=8, Cina=9)
- coefficienti componenti del modello (la scelta dei coefficienti, differenti fra le ragioni, si basa sul trend storico e le principali stime degli analisti):
- α: tasso di crescita intrinseco della regione (USA, Europa, Cina rispettivamente): la crescita negli USA è direttamente proporzionale al budget investito negli USA, ecc
- β: effetto competitivo nel breve termine (la crescita negli USA è accentuata dalla leadership rispetto agli altri quindi Europa, Cina)
- γ: beneficio a lungo termine della crescita complessiva (gli investimenti globali nel settore trainano l'intero settore quindi, nel lungo termine, tutti beneficiano di una crescita globale)
- δ: termine di saturazione per limitare la crescita (curva più ralistica, non può procedere proprio esponenziale nel lungo termine)
- aggiustamento con il tasso di inflazione (media stimata per i prossimi dieci anni): inflazione USA 2,5%, Europa 2%, Cina 2,5%; per semplicità nel calcolo, l'inflazione globale è stata calcolata come media aritmetica anziché media ponderata, considerati i valori simili (formalmente sarebbe più preciso fare una somma ponderata per il calcolo dell'impatto globale reale, ovvero al netto dell'inflazione)
- il modello procede con discretizzazione numerica ogni mese, per i prossimi 10 anni
- calibrazione parametri: in funzione del CAGR (tasso di crescita annuale composto), i dati che ho preso sono molto cautelativi, forse sottostimati in ottica di rallentamento della crescita vista la crescita già avvenuta (CAGR circa 12,5% quando secondo alcune stime potremmo anche considerare una media di 20% circa)
Quindi il modello assume la forma:
- dU1/dt = α1U1 + β1(U1-U2-U3) + γ1(U1+U2+U3) - δ1U12
- dU2/dt = α2U2 + β2(U2-U1-U3) + γ2(U1+U2+U3) - δ2U22
- dU3/dt = α3U3 + β3(U3-U1-U2) + γ3(U1+U2+U3) - δ3U32
Vediamo tutto il codice Python 3, per risolvere il modello (risoluzione numerica tramite metodo di Eulero esplicito), con i vari commenti al codice. I coefficienti sono stati definiti in questo caso in modo statico, all'interno della definizione delle funzioni, eventualmente si possono variare sia per cambiare le condizioni iniziali, sia come analisi di sensitività.
import numpy as np
import matplotlib.pyplot as plt
# Funzioni del modello (esempio semplificato)
def dU1_dt(U1, U2, U3):
return 0.22 * U1 - 0.03 * U2 - 0.03 * U3 - 0.001 * U1**2
def dU2_dt(U1, U2, U3):
return -0.03 * U1 + 0.17 * U2 - 0.03 * U3 - 0.001 * U2**2
def dU3_dt(U1, U2, U3):
return -0.03 * U1 - 0.03 * U2 + 0.19 * U3 - 0.001 * U3**2
# Parametri
dt = 1.0 / 12 # Passo mensile
T = 10 # 10 anni
n_steps = int(T / dt)
time = np.arange(0, T, dt)
# Array per i valori
U1 = np.zeros(n_steps)
U2 = np.zeros(n_steps)
U3 = np.zeros(n_steps)
U_total = np.zeros(n_steps)
# Condizioni iniziali
U1[0] = 10
U2[0] = 8
U3[0] = 9
U_total[0] = U1[0] + U2[0] + U3[0]
# Simulazione (metodo di Eulero)
for i in range(n_steps - 1):
U1[i + 1] = U1[i] + dU1_dt(U1[i], U2[i], U3[i]) * dt
U2[i + 1] = U2[i] + dU2_dt(U1[i], U2[i], U3[i]) * dt
U3[i + 1] = U3[i] + dU3_dt(U1[i], U2[i], U3[i]) * dt
U_total[i + 1] = U1[i + 1] + U2[i + 1] + U3[i + 1]
# Tassi di inflazione
r_USA = 0.025 # 2.5%
r_EU = 0.02 # 2%
r_CN = 0.025 # 2.5%
r_global = (r_USA + r_EU + r_CN) / 3 # Media
# Indici dei prezzi
P_USA = (1 + r_USA)**time
P_EU = (1 + r_EU)**time
P_CN = (1 + r_CN)**time
P_global = (1 + r_global)**time
# Valori reali
U1_real = U1 / P_USA
U2_real = U2 / P_EU
U3_real = U3 / P_CN
U_total_real = U_total / P_global
# Grafici
plt.figure(figsize=(12, 8))
# 1. U1, U2, U3 nominali
plt.subplot(2, 2, 1)
plt.plot(time, U1, label='U1 (USA)')
plt.plot(time, U2, label='U2 (Europa)')
plt.plot(time, U3, label='U3 (Cina)')
plt.title('Livello IA nominale per regione')
plt.xlabel('Tempo (anni)')
plt.ylabel('Livello IA')
plt.legend()
plt.grid(True)
# 2. U1, U2, U3 reali
plt.subplot(2, 2, 2)
plt.plot(time, U1_real, label='U1 reale (USA)')
plt.plot(time, U2_real, label='U2 reale (Europa)')
plt.plot(time, U3_real, label='U3 reale (Cina)')
plt.title('Livello IA reale per regione')
plt.xlabel('Tempo (anni)')
plt.ylabel('Livello IA reale')
plt.legend()
plt.grid(True)
# 3. U_total nominale
plt.subplot(2, 2, 3)
plt.plot(time, U_total, label='U1 + U2 + U3 nominale', color='purple')
plt.title('Livello IA globale nominale')
plt.xlabel('Tempo (anni)')
plt.ylabel('Livello IA globale')
plt.legend()
plt.grid(True)
# 4. U_total reale
plt.subplot(2, 2, 4)
plt.plot(time, U_total_real, label='U1 + U2 + U3 reale', color='purple')
plt.title('Livello IA globale reale')
plt.xlabel('Tempo (anni)')
plt.ylabel('Livello IA globale reale')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
Vediamo quindi il grafico che mostra i risultati: nella prima colonna, andamento nominale (delle singole regioni e globale); nella seconda colonna, andamento reale, al netto dell'inflazione.
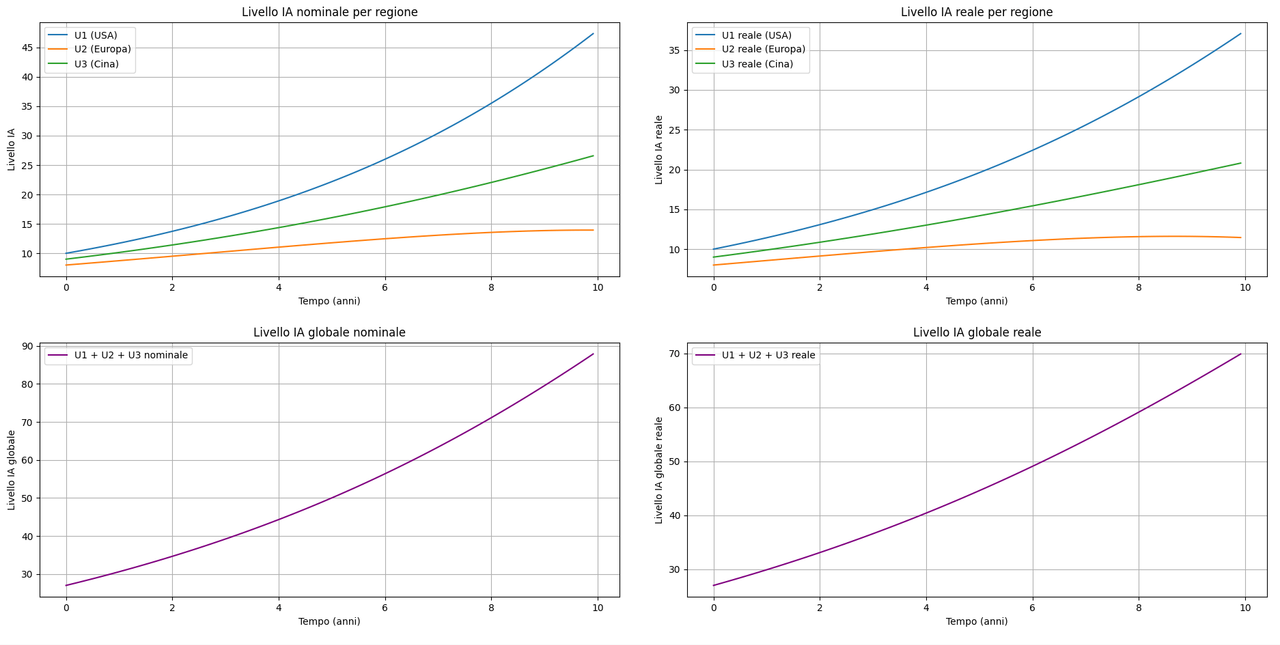
Conclusioni e osservazioni aggiuntive:
- il modello è ovviamente una semplificazione rispetto alla realtà, indica comunque un trend verosimile, suddiviso fra le regioni e considerando i principali parametri e relazioni
- interessante anche la correlazione Il prezzo del rame come indicatore dell'economia globale, vista la forte domanda per investimenti futuri, elettronica e quindi infrastruttura per IA, Data Center, la crescita del prezzo del rame (oggi al massimo storico) indica ottimismo riguardo alla continua crescita del settore
- considerazioni economiche sui risultati della simulazione:
- lato consumatore: la situazione di unico attore globale rappresenta monopolio; la situazione migliore per il consumatore è invece quella che più si avvicina ad una concorrenza perfetta, ovvero crescita globale del settore, competitiva (offerta di beni e servizi), quindi anche per questo settore
- lato investitore: in ottica lungo termine, la crescita globale consente maggiore sicurezza e solidità grazie alla diversificazione, inoltre vengono limitati, attenuati eventuali drawdown, crolli di mercato; la crescita di un solo attore, che quindi è forte nel breve termine e incontra i rischi di insostenibilità nel medio-lungo termine, è più indicata per speculazione di breve periodo