Vediamo un esempio interessante con Excel di Piano di Accumulo Capitale (PAC). Si tratta di una tipologia di investimento a medio-lungo termine, che abbatte il rischio e le fluttuazioni, dato che andiamo a versare una somma (costante o variabile a seconda dei casi) su base periodica (es. mensile), per un certo orizzonte temporale.
Per il caso di studio è stato considerato l'indice NEF - Euro Equity R (nef.lu), dal 1 gennaio al 1 luglio 2023. Consideriamo quindi due interessanti tipologie di investimento (accenno anche ad una terza, che però escludiamo in quanto non rientrerebbe nemmeno nei PAC):
- investimento con rata costante: semplice, ogni mese investiamo la stessa quantità di denaro nel fondo, indipendentemente se il mercato sale o scende
- investimento con rata adattiva: una soluzione migliorata (poi vediamo infatti le performance!), significa investire di più quando il mercato scende (quotazione bassa), investire di meno quando il mercato sale (quotazione alta). Ho personalmente definito una formula:
Qi=Q0*Y0/Yi, dove Qi è la rata al mese i-esimo che dobbiamo investire, Q0 il riferimento iniziale (ad esempio 100 euro mensili), Y0 la quotazione iniziale di quando siamo entrati sul mercato, Yi la quotazione al mese i-esimo, attuale (nella pratica, alcuni giorni prima di investire in quel mese anche perché dobbiamo comunicare alla banca l'eventuale variazione). La ragione di questa scelta è presto spiegata:
- se il mercato sale, la quotazione aumenta, dobbiamo investire meno, perché se poi scende noi perdiamo in percentuale quanto abbiamo investito prima (quindi il nostro precedente investimento "pesa in modo negativo")
- se il mercato scende, la quotazione diminuisce, investiamo di più perché in ottica lungo termine (quando il mercato sale, il trend generale è di crescita) il nostro guadagno è dato dalla differenza di prezzo. Guarda caso proprio Albert Einstein diceva: <<la crisi è la più grande benedizione per le persone e le nazioni>>
investimento in unica rata iniziale: questo lo escludiamo a priori perché dipende fortemente dal "timing", quindi nella pratica è più una questione di fortuna che di strategia
La quotazione del fondo, da gennaio 2020 fino a luglio 2023 (quindi vengono evidenziati anche i cali dovuti a Covid e guerra Russia-Ucraina), è la seguente, mese per mese rappresentato in un vettore:
EuroEquityR=[17.35,17.31,16.07,13.13,14.61,15.4,16.26,16.24,17.07,17.05,15.97,18.56,18.75,18.54,19.29,20.19,20.72,21.44,21.73,22.39,23.06,21.89,23.16,23.60,23.95,21.82,19.67,20.91,19.92,19.32,17.52,19.90,18.01,17.26,18.24,19.98,18.97,20.97,21.14,21.44,21.23,21.70,21.89]
PAC: implementazione con foglio di calcolo
Fatta questa premessa, vediamo un'implementazione (non Excel ma LibreOffice Calc, considerazioni comunque analoghe 😀). Per semplicità mostro i risultati con questa strada anziché un programma in Python, C/C++ o altro che sia.
Vediamo come dev'essere strutturato questo (complesso) foglio di calcolo:
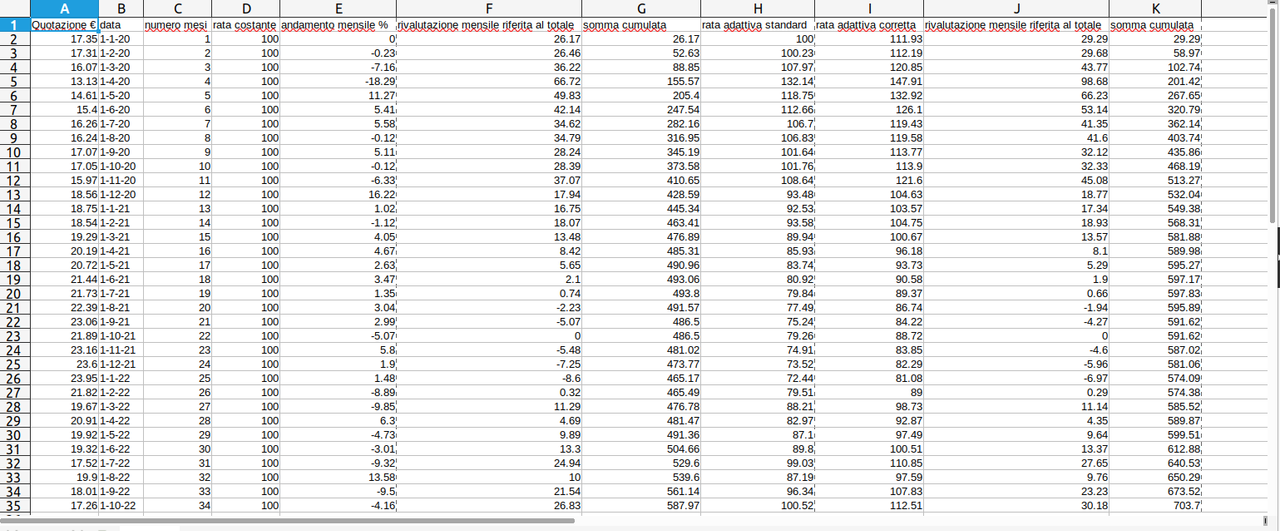
- colonna A: quotazione
- colonna B: data
- colonna C: numero progressivo dei mesi
- colonna D: rata costante (volendo poteva bastare un'unica cella, è uguale)
- colonna E: andamento mensile in percentuale (rata costante): nella prima cella mettiamo 0, nella seconda cella la formula è
=ROUND(D3*(A3-A2)/A2,2), approssimo a due cifre decimali; quindi indica la quotazione meno la quotazione precedente, diviso la quotazione precedente (appunto variazione percentuale)
- colonna F: rivalutazione mensile riferita al totale (rata costante): la formula è
=ROUND(D2*($A$44-A2)/A2,2), qui stiamo virtualmente considerando quanto impatta nel tempo di riferimento finale l'investimento di ogni mese (A44 infatti è l'ultima cella, 1 luglio 2023)
- colonna G: somma cumulata (rata costante) della colonna F, quindi questo ci mostra l'andamento mensile, quando siamo all'ultimo mese possiamo tirare le conclusioni sull'investimento complessivo
- colonna H: rata adattiva standard: partendo da Q0=100, come detto prima la formula è
=ROUND($D$3*($A$2/A3),2); l'ho chiamata "standard" poiché alla fine, facendo la somma dei 43 mesi, otteniamo 3841,63€ che NON è uguale ai 4300€ del caso rata costante pari a 100€; quindi ci torna utile poi la prossima colonna
- colonna I: rata adattiva corretta: con la formula
=ROUND(H2*$D$46/$H$46,2) in pratica applichiamo il fattore correttivo, altrimenti non avrebbe poi senso confrontare i due diversi investimenti, rata costante e rata adattiva; in questo modo invece moltiplico la rata adattiva standard per 4300/3841,63 e quindimi permette (a posteriori) di avere confrontabilità, la somma totale investita nell'intero periodo (2020-2023) per i due diversi investimenti coincide
- colonna J: rivalutazione mensile riferita al totale (rata adattiva): formula
=ROUND(I2*($A$44-A2)/A2,2), è l'analogo del caso precedente
- colonna K: somma cumulata (rata adattiva): formula
=SUM($J$2:J2), analogo del caso precedente, tiene già conto del fattore correttivo
Risultati:
- rata costante: alla fine del periodo otteniamo 646,96€
- rata adattiva: alla fine del periodo otteniamo 762,9€
A parte l'esempio numerico, concettualmente è importante capire quindi l'importanza di una strategia di questo tipo, investire in modo adattivo per ottimizzare la resa di un PAC: investire di più quando il mercato è basso, investire di meno quando il mercato è alto.
Vediamo ora due immagini, la prima mostra i tre grafici (andamento della quotazione Euro Equity R, dal 1 gennaio 2020 al 1 luglio 2023, poi il grafico dell'investimento con rata costante e infine quello con rata adattiva), la seconda immagine invece mostra la schermata del foglio di calcolo.