Il concetto di calcolo distribuito può essere qualcosa di davvero utile, unire la potenza computazionale di due o più computer. Possiamo farlo ad esempio a livello di rete locale (LAN) oppure rete globale (come ho fatto io nell'esempio che segue, tramite Dropbox).
Il concetto base è questo: ottimizzazione della linea temporale! Vale a dire che ogni macchina sfrutta la propria potenza di calcolo (e in alcuni casi può essere rilevante anche in termini di memoria allocata), anziché eseguire la totalità delle operazioni (una dopo l'altra) ne esegue una parte e nello stesso tempo un'altra macchina esegue delle operazioni in parallelo. Poi l'algoritmo dev'essere scritto in modo tale da gestire e sfruttare al meglio questa sovrapposizione. Vediamo poi i dettagli.
Il caso che ho voluto studiare, l'ho impostato in questo modo:
- Dropbox, per creare una cartella condivisa fra i due computer (quindi potenzialmente una rete globale, non solo locale)
- Linux Mint sul computer principale (programma chiamato diff2.c)
- Linux ParrotOS sul computer secondario (programma chiamato diff1.c)
Nello specifico, il mio algoritmo in C fa parte dell'analisi numerica, equazione differenziale della diffusione 1D tramite metodo FTCS, simile a quanto abbiamo già visto nel caso dell'equazione della diffusione, metodo FTCS numerico - Python Matplotlib. Più in dettaglio, vediamo i due programmi:
- diff1.c calcola un certo numero di iterazioni e stampa poi su file l'output chiamato "outputNP.txt" (NP = non preciso, un nome di riferimento che ho dato io); poi questo programma semplicemente termina
- diff2.c calcola il doppio delle ierazioni del precedente, avendo passo di discretizzazione dimezzato, questi valori rimangono nella RAM; dopodiché acquisisce in input l'array stampato dall'altro programma e crea una combinazione lineare VC=2VP-VNP (sovrascrivendo l'array memorizzato nella RAM, V ovvero VP si sovrascrive originando quanto ora ho definito VC) per fornire poi come risultato "outputC.txt" (C = corretto, un nome di riferimento per indicare che l'algoritmo è più accurato).
NB: il caso in esame è solo un esempio (il programma calcola i valori con dei dati di esempio, ovviamente), rende già l'idea delle potenzialità. Le iterazioni qui non sono molte, l'esecuzione termina in pochi secondo quindi è abbastanza irrilevante la cosa. Pensando però di aumentare il tempo di esecuzione del codice, potremmo avere un algoritmo anche molto più complesso, che richiede diversi minuti o anche ore di esecuzione! In quel caso, avere due macchine in parallelo abbatte notevolmente il tempo di esecuzione (il tempo speso per l'acquisizione del risultato di uno, è notevolmente inferiore rispetto al tempo totale di esecuzione, quindi è conveniente).
Riportiamo ora i due programmi scritti in linguaggio C.
Questo è il codice di diff1.c (programma che termina la propria esecuzione):
//FDM FTCS 1D Diffusion Equation (delta=deltaNP)
#include <stdio.h>
int main() {
register unsigned short Tout=1000;
register float delta=0.1; //deltaNP=0.1, deltaP=0.05
register unsigned short L=10;
register float C0=100;
register float dx=0.1;
register float D=0.5;
register float dt=delta*dx*dx/D;
register unsigned int i=0;
register float k=0;
float V[(int)(L/dx)];
//init
for(i=0;i<(int)(L/dx);i++){
V[i]=0;
}
V[0]=C0;
//loop
while(k<Tout){
for(i=1;i<(int)(L/dx)-1;i++){
V[i]+=delta*(V[i+1]-2*V[i]+V[i-1]);
}
k+=dt;
}
//stampa su file outputNP
FILE *f1=fopen("outputNP.txt","w");
for(i=0;i<(int)(L/dx);i++){
fprintf(f1,"%f\n",V[i]);
}
fclose(f1);
return 0;
}
Questo invece è il codice di diff2.c (programma che poi continua acquisendo come input i risultati dell'altro):
//FDM FTCS 1D Diffusion Equation (delta=deltaP)
#include <stdio.h>
int main() {
register unsigned short Tout=1000;
register float delta=0.05; //deltaNP=0.1, deltaP=0.05
register unsigned short L=10;
register float C0=100;
register float dx=0.1;
register float D=0.5;
register float dt=delta*dx*dx/D;
register unsigned int i=0;
register float k=0;
float V[(int)(L/dx)]; //V=VP
float Vnp[(int)(L/dx)]; //VNP, acquisizione dell'altro file
//init
for(i=0;i<(int)(L/dx);i++){
V[i]=0;
}
V[0]=C0;
//loop
while(k<Tout){
for(i=1;i<(int)(L/dx)-1;i++){
V[i]+=delta*(V[i+1]-2*V[i]+V[i-1]);
}
k+=dt;
}
//acquisizione da file outputNP
FILE *f1=fopen("outputNP.txt","r");
for(i=0;i<(int)(L/dx);i++){
fscanf(f1,"%f\n",&Vnp[i]);
}
fclose(f1);
//calcolo VC=2VP-VNP (sovrascrivo VP[i])
for(i=0;i<(int)(L/dx);i++){
V[i]=2*V[i]-Vnp[i];
}
//stampa su file output VC
FILE *f2=fopen("outputC.txt","w");
for(i=0;i<(int)(L/dx);i++){
fprintf(f2,"%f\n",V[i]);
}
fclose(f2);
return 0;
}
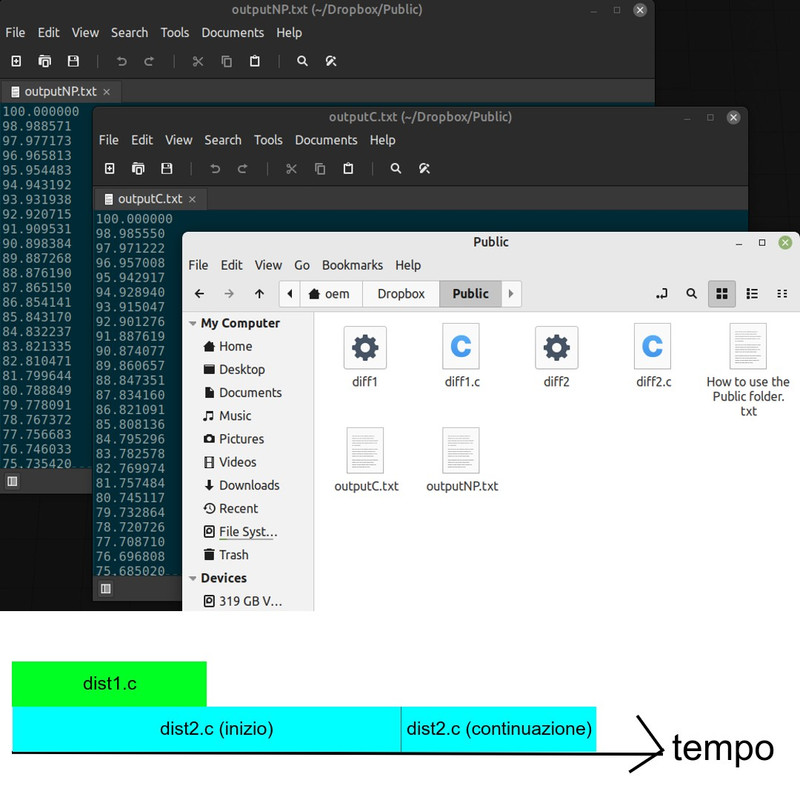
Infine un'immagine, che mostra lo screenshot dei risultati (visualizzato da Linux Mint, dove è stato eseguito diff2.c, programma che arriva poi alla conclusione) e sotto la rappresentazione della timeline, per aver chiaro il concetto: il beneficio che ottengo dal calcolo distribuito è rappresentato dalla sovrapposizione della linea temporale, cosa che con un unica macchina non potrei avere!!! (nell'immagine ho scritto"dist", si intende "diff", semplicemente prima avevo assegnato un nome diverso ai file, il concetto non cambia). Spero vi piaccia e renda l'idea! 😀