Dopo aver visto un caso visivamente simile in 3D, che è ricerca strada di ottimizzazione (Adventofcode) - distribuzione altimetrica così come il caso 2D Python Matplotlib - Random Walk ("passeggiata aleatoria"), vediamo ora qualcosa di simile ovvero come creare un rilievo montuoso con Python-Matplotlib. Lo scopo in questo caso non era quello di assegnare un valore random ad ogni cella, bensì creare una matrice e assegnare valore massimo al centro (pari a Nx*Ny/4), diventando inversamente proporzionale avvicinandosi ai bordi (pari a zero lungo tutto il bordo).
Il codice è il seguente:
import numpy as np
from matplotlib import pyplot as plt
Nx=20
Ny=20
Z=np.zeros((Nx,Ny))
for j in range(0,Ny):
for i in range(0,Nx):
if(i>=int(Nx/2) and j>=int(Ny/2)):
Z[i][j]=(Ny-j)*(Nx-i)
elif i>=int(Nx/2) and j<int(Ny/2):
Z[i][j]=(Nx-i)*j
elif j>=int(Ny/2) and i<int(Nx/2):
Z[i][j]=i*(Ny-j)
elif i<int(Nx/2) and j<int(Ny/2):
Z[i][j]=i*j
plt.figure()
ax = plt.axes(projection ='3d')
for j in range(Ny):
for i in range(Nx):
ax.bar3d(i, j, 0, 1, 1, Z[i][j], color="green")
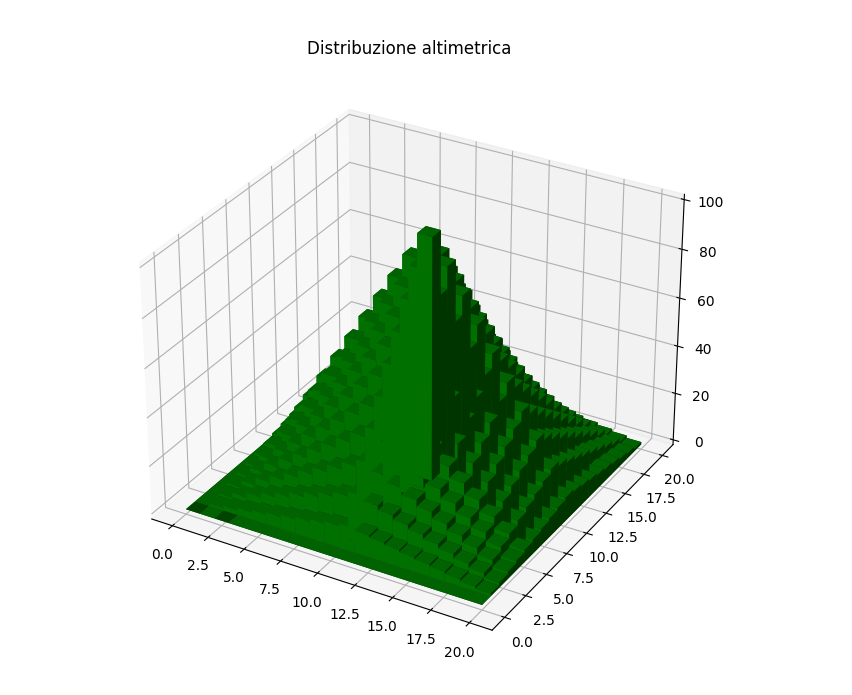
plt.title("Distribuzione altimetrica - esempio rilievo montuoso")
plt.show()
Questa è l'immagine del grafico (tramite istogrammi), che può rendere l'idea di una possibile applicazione pratica (più che un rilievo montuoso questo screenshot sembra una costruzione dei LEGO 😄).