Abbiamo visto come creare grafici 3D con Matplotlib, libreria Python. Vediamo ora un caso di applicazione dell'analisi complessa.
L'analisi complessa è il campo della matematica che studia funzioni con dominio nell'insieme dei numeri complessi, ovvero:
- Re(z) = parte reale
- Im(z) = parte immaginaria
La necessità di estendere la matematica oltre ai numeri reali nasce da alcune esigenze, come calcolare la soluzione di x2+1=0, che determina x2=-1, non ammette soluzioni nei numeri reali, mentre la soluzione complessa è x=±i, con "i" = unità immaginaria (creata appositamente per lo scopo).
Un numero complesso del tipo Z è esprimibile con la forma: Z=a+b(i), ovvero Re(z)=a, Im(z)=b. Questo può essere rappresentato su un piano cartesiano "speciale", il piano di Gauss, in modo analogo alle classiche funzioni nel dominio reale a cui siamo abituati.
Solitamente quindi nel piano complesso si ha questa situazione: un numero complesso è un punto del piano (x,y sono Re(z) e Im(z)).
Caso di studio: esponenziale complesso
In questo caso abbiamo quindi un numero complesso dipendente dal tempo, z=z(t): z=exp(-it)
Per le proprietà dei numeri complessi, scriviamo: exp(-it) = cos(t) -i * sin(t)
Quindi si ottiene:
Re(z) = cos(t)Im(z) = sin(t)
Con Python e Matplotlib costruiamo un grafico a dispersione; per ogni tempo (t = 0, ... 1) avremo dei punti nel grafico, l'insieme di questi punti determina appunto l'andamento nel tempo quindi la funzione z(t)=exp(-it). Il codice è il seguente:
#exp(-i*t)=cos(t)-i*sin(t)
import numpy as np
from matplotlib import pyplot as plt
plt.figure()
ax = plt.axes(projection ='3d')
t = np.linspace(0, 1, 100)
x = np.cos(t)
y = -np.sin(t)
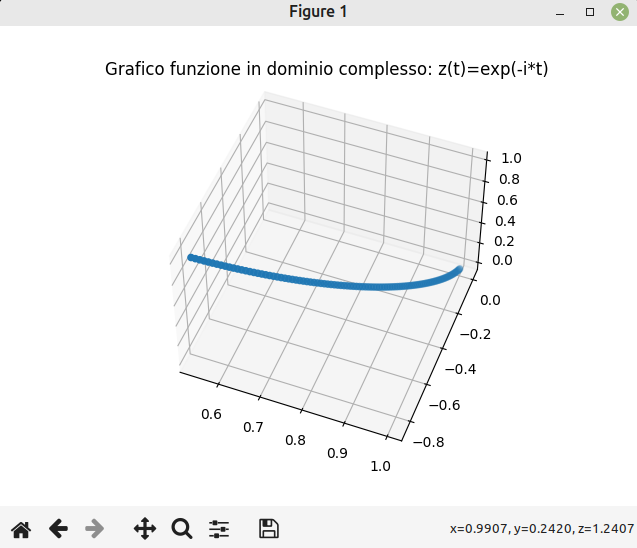
plt.title("Grafico funzione in dominio complesso: z(t)=exp(-i*t)")
ax.scatter(x, y, t)
plt.show()
Infine la rappresentazione della funzione, tramite grafico a dispersione.