Abbiamo già visto alcuni esempi con la libreria Matplotlib di Python, ad esempio la risoluzione numerica tramite FTCS dell'equazione della diffusione.
Vediamo ora sempre un caso di analisi numerica, l'equazione differenziale di Burgers (Burgers' Equation), che si può scrivere nel modo seguente:

Per l'esempio in questione, è stato scelto il metodo numerico di Godunov e questi dati di partenza:
- condizione iniziale "a gradino", q0=1, nel resto del dominio zero
- delta=0.5=costante
- esempi aumentando il numero di iterazioni
Di seguito il codice Python:
import numpy as np
from matplotlib import pyplot as plt
#dq/dt+q*dq/dx=0
N=100
q0=1
V=np.zeros(N)
V[0]=q0
delta=0.5
#dt=delta*dx/q
for k in range(0,5):
for i in range(1,N):
V[i]+=-delta*(V[i]-V[i-1])
plt.figure()
plt.title("Burgers' Equation, delta = 0.5, k = 5 iterazioni")
x = np.linspace(0, 10, N)
plt.plot(x,V)
plt.show()
Mostriamo l'output grafico del caso con 5 iterazioni (quindi, vicino alla situazione iniziale di condizione "a gradino"):
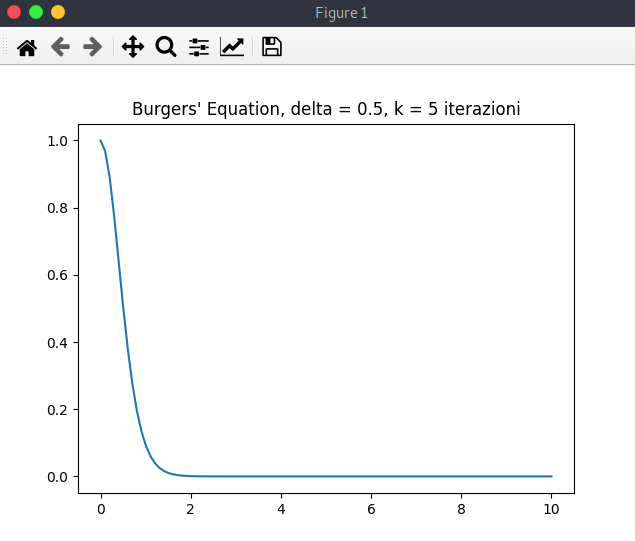
Ora l'output con 50 iterazioni:
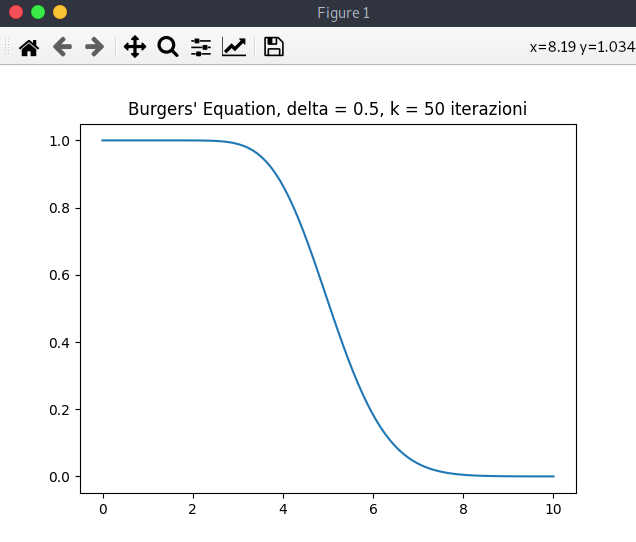
Infine l'outplut con 150 iterazioni:
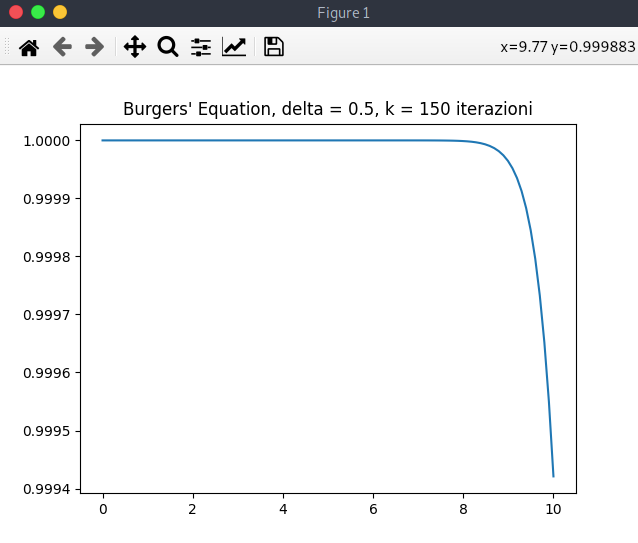
Si vede quindi l'andamento. Il frangimento delle onde segue dinamiche di questo tipo. Aumentando delta fino al massimo valore di stabilità (0<delta<1, derivando dal "numero di Courant" e avendo scelto questo metodo numerico), si nota che viene raggiunta prima la condizione, con meno iterazioni ma anche con minore accuratezza dato che la soluzione numerica risulterebbe più approssimata; di fatto in funzione di delta si calcola l'incremento temporale dt (abbiamo semplicemente parlato di iterazioni, in questo caso ad ogni iterazione corrisponde un aumento di tempo, che non è costante essendo variabile in base al valore di q(x,t) ovvero nel codice V[ i ] ).
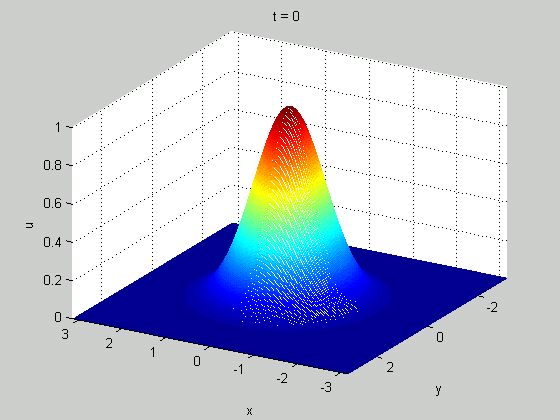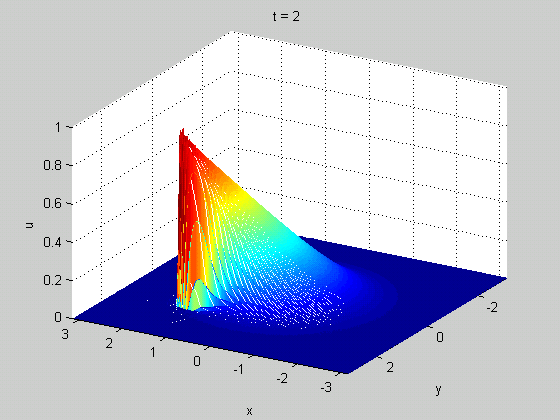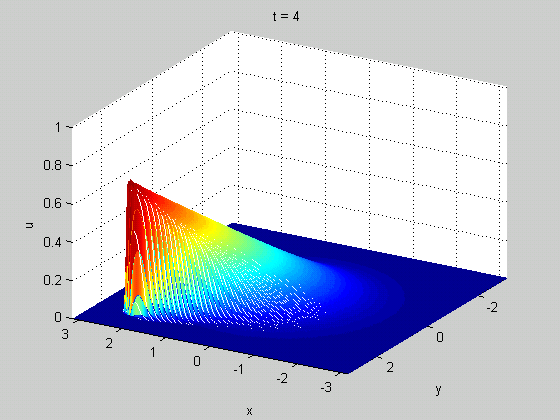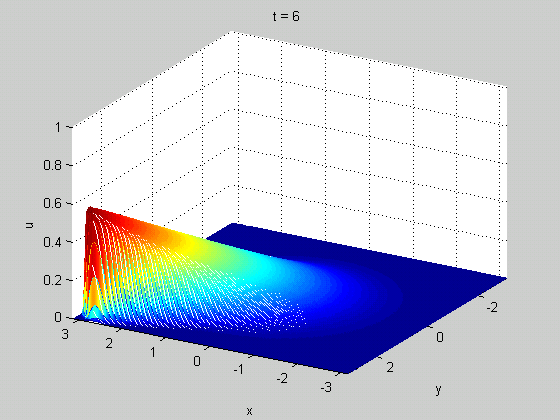
Per quanto riguarda il frangimento delle onde, ancora più rappresentativa l'animazione 3D tratta da Wikipedia: