Abbiamo già visto un caso di analisi complessa con Python, era un caso semplice in cui in modo facile si riuscivano a separare le componenti Re(z) e Im(z) del numero complesso z, definito da una certa funzione f(z), dove z=Re+i*Im, i è l'unità immaginaria.
Mostriamo ora il codice per risolvere una situazione generale di non linearità, la funzione è stata scelta piuttosto "a caso" e il grafico mostrato tramite Heatmap.
Nel codice che segue, per adattarlo al caso desiderato occorre modificare la funzione z(x,y,ic=1) nel "return", indicando la funzione desiderata. Abbiamo chiamato "ic" l'unità immaginaria (assegnando valore 1 arbitrario, che occorre per il codice che segue) per non confonderla con "i" solitamente usato come contatore in un ciclo. Di conseguenza, dato che un numero complesso è esprimibile tramite z=Re(z)+i*Im(z), facendo "virtualmente" la derivata rispetto all'unità immaginaria, si ottiene Im(z) e di seguito Re(z)=z-Im(z).
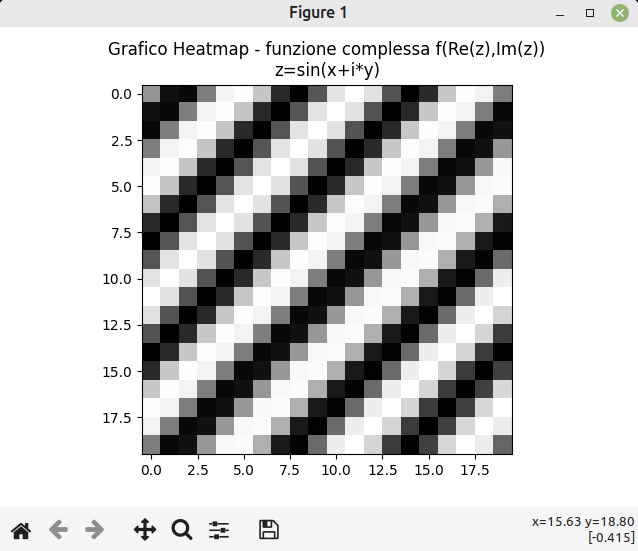
Ecco mostrato il codice di questa strana funzione, z=sin(x+i*y).
import numpy as np
from matplotlib import pyplot as plt
def z(x,y,ic=1):
return np.sin(x+ic*y)
def Im(x,y):
return (z(x,y,ic=1+1e-8)-z(x,y,ic=1))/(1e-8)
def Re(x,y):
return z(x,y,ic=1)-Im(x,y)
N=20
V=np.zeros((N,N))
color='Greys'
for j in range(N):
for i in range(N):
V[i][j]=z(Re(i,j),Im(i,j),ic=1)
plt.imshow(V,color)
plt.title("Grafico Heatmap - funzione complessa f(Re(z),Im(z))\nz=sin(x+i*y)")
plt.show()
Di seguito l'immagine tramite Heatmap, in scala di grigi.