È noto che parchi e foreste agiscano come "polmoni verdi" per le aree urbane. Questo articolo si propone di quantificarne l'effetto attraverso un caso di studio: quanto velocemente un'area verde può assorbire un picco di inquinamento da CO2.
In prima fase, la creazione di un modello matematico, sistema di equazioni differenziali; in seguito codice Python, simulazione e analisi dei risultati.
Modello matematico
Il modello prevede una coppia di equazioni differenziali:
d[CO2]/dt = -k * [CO2]d[O2]/dt = +k * [CO2]
Vale a dire che la concentrazione di CO2 decade con una cinetica di primo ordine; la produzione di ossigeno è proporzionale al consumo di CO2 (dato che, dalla reazione 6CO₂ + 6H₂O → C₆H₁₂O₆ + 6O₂ viene evidenziato rapporto molare fra CO2 consumata e O2 prodotta pari a 1:1). Per semplicità, ipotesi che la concentrazione di CO2 non è così elevata da saturare la capacità fotosintetica delle piante (altrimenti occorre un modello più complesso, es. Michaelis-Menten).
Per quanto riguarda i parametri chiave:
- la costante k, molto importante, rappresenta l' "efficienza" della superficie verde, stimata in base agli altri parametri
- V: volume di controllo, 1 km2 di superficie per 100 m di altezza, ipotesi di miscelazione perfetta, uniforme
- J: flusso di assorbimento, valore medio preso in letteratura (foresta temperata, giornata di sole)
- LAI (Leaf Area Index): una superficie verde perfettamente piatta ha LAI=1, mentre il LAI indica quanti m2 di superficie fogliare ci sono per ogni m2 di suolo
- CO2 iniziale: anziché la media atmosferica di 420 ppm, consideriamo una "bolla inquinata" di 2000 ppm, quindi ad esempio foresta vicino ad una città inquinata; approfondimento:
- prato ben curato: LAI 1 - 2
- campo di mais maturo: LAI 3 - 4
- foresta decidua temperata (in estate): LAI 4 - 6 (per questo caso di studio si è scelto un valore rappresentativo di LAI=5)
- foresta di conifere: LAI 5 - 8
- foresta pluviale tropicale: LAI 8 - 12
Codice Python e simulazione
Con l'aiuto dell'IA, gemini-2.5-pro, ecco il codice Python completo per il caso di studio e a seguire lo screenshot del grafico.
import numpy as np
import matplotlib.pyplot as plt
# --- 1. Parametri del Modello Migliorato ---
# Parametri fisici del sistema
A_suolo = 1e6 # Area del suolo [m^2] (1 km^2)
LAI = 5.0 # Leaf Area Index per una foresta temperata [adimensionale]
A_fogliare = A_suolo * LAI # Superficie fogliare totale [m^2]
h_volume = 100 # Altezza del volume di controllo [m]
V = A_suolo * h_volume # Volume di controllo [m^3]
# Parametri della fotosintesi e ambientali
J = 10e-6 # Flusso di assorbimento di CO2 per m^2 di foglia [mol/(m^2*s)]
R = 8.314 # Costante dei gas [J/(mol*K)]
T = 298.15 # Temperatura [K]
# --- 2. Stima della costante 'k' per la nostra foresta ---
# Usiamo la concentrazione di riferimento (420 ppm) per stimare k,
# che rappresenta la 'potenza' intrinseca della nostra foresta.
CO2_ref_ppm = 420
P_atm = 101325 # Pressione atmosferica [Pa]
P_co2_ref = CO2_ref_ppm * 1e-6 * P_atm
CO2_ref_mol_m3 = P_co2_ref / (R * T)
# k rappresenta l'efficienza di rimozione della foresta
k = (J * A_fogliare) / (V * CO2_ref_mol_m3)
print(f"Stima del LAI: {LAI}")
print(f"Superficie fogliare equivalente: {A_fogliare:.2e} m^2")
print(f"Stima della costante di velocità 'k': {k:.2e} s^-1")
print("-" * 40)
# --- 3. Condizioni Iniziali per lo Scenario ad Alta CO2 ---
# Scenario "zona inquinata"
CO2_0_ppm = 2000
P_co2_0 = CO2_0_ppm * 1e-6 * P_atm
CO2_0 = P_co2_0 / (R * T)
# Concentrazione di O2 rimane quella standard (assumiamo inquinamento locale da CO2)
O2_0_percent = 0.2095
P_o2_0 = O2_0_percent * P_atm
O2_0 = P_o2_0 / (R * T)
print(f"Scenario: Alta CO2")
print(f"Concentrazione CO₂ iniziale: {CO2_0:.4f} mol/m³ ({CO2_0_ppm} ppm)")
print(f"Concentrazione O₂ iniziale: {O2_0:.4f} mol/m³")
print("-" * 40)
# --- 4. Simulazione nel tempo ---
# Vettore del tempo: simuliamo per 3 giorni, che dovrebbero bastare
# vista la maggiore velocità di rimozione.
t_giorni = 3
t_max_secondi = t_giorni * 24 * 3600
t = np.linspace(0, t_max_secondi, 1000)
# --- 5. Soluzioni Analitiche ---
co2_t = CO2_0 * np.exp(-k * t)
o2_t = O2_0 + CO2_0 - co2_t
# --- 6. Creazione del Grafico ---
t_ore = t / 3600
fig, ax1 = plt.subplots(figsize=(12, 7))
color_co2 = 'tab:red'
ax1.set_xlabel('Tempo (ore)')
ax1.set_ylabel('Concentrazione CO₂ (mol/m³)', color=color_co2)
# Aggiungiamo un riferimento orizzontale al livello atmosferico standard
ax1.axhline(y=CO2_ref_mol_m3, color=color_co2, linestyle=':', label=f'Livello CO₂ standard ({CO2_ref_ppm} ppm)')
ax1.plot(t_ore, co2_t, color=color_co2, linewidth=2.5, label='CO₂(t) - Scenario Alta [CO₂]')
ax1.tick_params(axis='y', labelcolor=color_co2)
ax1.grid(True, linestyle='--', alpha=0.6)
ax2 = ax1.twinx()
color_o2 = 'tab:blue'
ax2.set_ylabel('Concentrazione O₂ (mol/m³)', color=color_o2)
ax2.plot(t_ore, o2_t, color=color_o2, linewidth=2.5, label='O₂(t)')
ax2.tick_params(axis='y', labelcolor=color_o2)
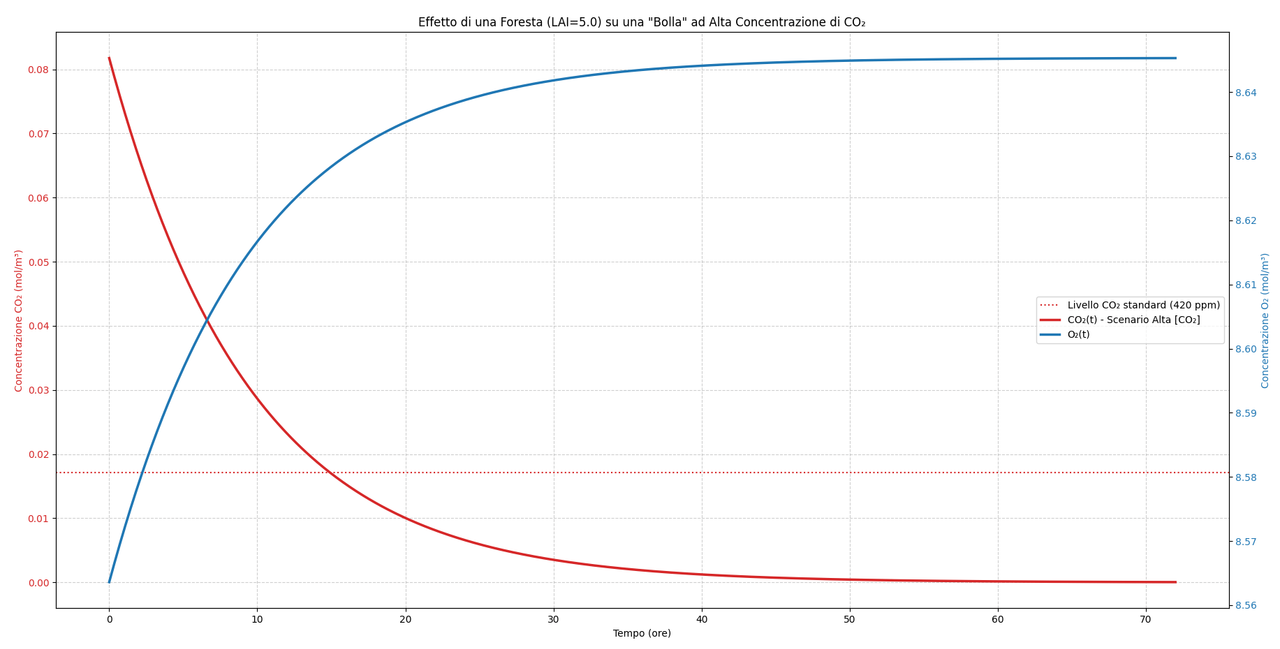
plt.title(f'Effetto di una Foresta (LAI={LAI}) su una "Bolla" ad Alta Concentrazione di CO₂')
lines, labels = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines + lines2, labels + labels2, loc='center right')
fig.tight_layout()
plt.show()
# --- 7. Stampa di alcuni risultati numerici ---
tempo_caratteristico_ore = (1/k) / 3600
print(f"Il tempo caratteristico di decadimento (riduzione del 63%) è di circa {tempo_caratteristico_ore:.1f} ore.")
# Calcoliamo dopo quanto tempo la CO2 torna al livello standard
# co2_t = CO2_0 * exp(-k*t_obiettivo) => t_obiettivo = -ln(co2_t / CO2_0) / k
if co2_t[-1] < CO2_ref_mol_m3:
t_obiettivo_s = -np.log(CO2_ref_mol_m3 / CO2_0) / k
t_obiettivo_h = t_obiettivo_s / 3600
print(f"Il tempo per tornare al livello standard di CO2 è di circa {t_obiettivo_h:.1f} ore.")
else:
print(f"Dopo {t_giorni} giorni, la concentrazione di CO2 è ancora sopra il livello standard.")
Analisi dei risultati
Dal grafico e dai dati generati emergono osservazioni significative. In primo luogo, l'efficacia della foresta nel ridurre la CO2 è notevole: il modello stima che la concentrazione scenda dal picco di 2000 ppm al livello atmosferico standard in circa 15 ore. Questo quantifica in modo tangibile la capacità di mitigazione di un ecosistema sano.
In secondo luogo, il ruolo del Leaf Area Index (LAI) si rivela determinante. Un valore di LAI=5, tipico di una foresta, implica una superficie fotosintetica cinque volte superiore a quella del suolo, accelerando di conseguenza il processo di assorbimento. Infine, il doppio asse Y evidenzia come, a fronte di un drastico calo relativo della CO₂, l'aumento dell'O2 sia minimo in rapporto alla sua abbondanza atmosferica, un risultato fisicamente coerente.
Conclusioni
Il modello differenziale, pur basandosi su ipotesi semplificative, si dimostra uno strumento potente per ottenere una stima quantitativa dell'impatto ecologico di un'area verde. Le principali semplificazioni includono la costanza della costante k (che nella realtà dipende dal ciclo giorno/notte e da altri fattori ambientali) e l'assenza di un meccanismo di saturazione della fotosintesi.
Nonostante questi limiti, la simulazione fornisce un ordine di grandezza realistico e sottolinea in modo inequivocabile l'importanza strategica della conservazione e della creazione di aree verdi dense (con LAI elevato) per la mitigazione dell'inquinamento atmosferico locale.