Non era semplice scegliere il titolo per questo studio che ho fatto, nella descrizione diventerà tutto più comprensibile. Il concetto di base è questo, come studio fatto a priori: dato un certo asset, posso investire un certo capitale con ipotesi di un certo delta (positivo quindi take-profit o negativo quindi stop-loss); avrò dei costi di commissione (generalmente fisso+variabile), imposti dall'emittente, intermediario (ad esempio, la mia banca).
Brevemente, nel caso di un'operazione in perdita, la perdita totale sarà data da capitale * delta + commissioni, mentre in caso di guadagno, il guadagno totale (lordo, consideriamo quindi il lordo, per il netto poi in Italia la tassazione sulla plusvalenza per l'azionario è pari al 26%) sarà invece capitale * delta - commissioni.
Quindi, se non ci fossero le commissioni, per andare in profitto sarebbe semplicemente sufficiente una probabilità di successo maggiore del 50%. Essendoci le commissioni, il valore sarà diverso e lo possiamo calcolare preventivamente in funzione del capitale e delta (quindi statisticamente sui grandi numeri, ad esempio se un indicatore mostra forte ipercomprato può essere più probabile la buona riuscita dell'operazione, viceversa se c'è molta incertezza, statisticamente - se pensiamo ad un trading quindi di breve periodo - avrebbe poco senso fare l'operazione).
Quindi, definiamo queste variabili:
- CAP = capitale da investire
- DELTA = percentuale di variazione (in positivo o negativo)
- COMM = commissioni totali
Statisticamente sui grandi numeri, andiamo in profitto se:
alfa*CAP*delta-COMM - (1-alfa)*(CAP*delta+COMM) > 0,
alfa quindi indica la probabilità minima per cui ci conviene statisticamente rischiare l'investimento, con quei dati; da questa disuguaglianza, ricavo alfa
Ecco a seguire un codice Python per calcolare alfa, in funzione dei vari parametri. Ovviamente anche COMM (costi di commissione) li ho definiti secondo una certa funzione matematica, fisso+variabile, vanno poi adeguati alle effettive tariffe del nostro intermediario, banca. Nota: le commissioni sono per ogni operazione, quindi entrata+uscita, per questo poi la formula diventa: alfa=0.5*(1+2*COMM(CAP)/(CAP*delta))
def COMM(CAP,MIN,MAX,percent): # calcolo commissioni
ris=percent*CAP
if(ris<MIN):
ris=MIN
elif(ris>MAX):
ris=MAX
ris+=2.3 # 2.3 euro = spese di borsa, extra
return ris
CAP=5000 # capitale da investire
MIN=7 #min = 7 euro
MAX=21 # max = 21 euro
percent=0.0015 # 0,15% spesa variabile fra MIN e MAX
delta=0.01 # delta = +-1%
alfa=0.5*(1+2*COMM(CAP,MIN,MAX,percent)/(CAP*delta)) # nota: commissioni all'entrata e uscita
print("alfa >",alfa)
Con i dati di studio, vediamo quindi alcuni esempi:
- 5000 euro, ±1%: alfa>0,696 --> ovvero ha senso investire se la probabilità di successo è maggiore del 70% circa
- 5000 euro, ±2%: alfa>0,598 --> 60% circa
- 10000 euro, ±1%: alfa>0,673
- 10000 euro, ±2%: alfa>0,586
Possiamo quindi vedere che il capitale dev'essere oltre un certo limite inferiore, ad esempio nel mio caso di studio questo è pari a 7/0,0015 = 4667 euro, dato che la spesa fissa minima è di 7 euro (da aggiungersi poi ai 2,3 euro di spese di borsa); quindi investire meno di questa cifra, ci porterebbe in condizione di svantaggio poiché le commissioni hanno un peso maggiore. Viceversa 21/0,0015 = 14000 euro, oltre i 14000 euro la spesa è fissa, sempre pari a 21 euro (ovviamente sempre in aggiunta ai 2,3 euro delle spese di borsa). Quindi investire un capitale maggiore, così come avere maggiore flessibilità su delta (attendere fino ad avere variazioni positive o variazioni negative più elevate), ci consente di ottenere un valore alfa più basso, che tende asintoticamente al 50% anziché essere a valori troppo alti (un valore più basso è preferibile, significa che per andare in profitto statisticamente è sufficiente individuare correttamente una percentuale più bassa di operazioni, il 60% piuttosto che il 70%, ecc).
Nel caso volessimo un esempio più dinamico, quindi con scelte differenti di capitale e delta (±1%, ±2%, ±3%), possiamo scrivere il codice che segue, eventualmente poi personalizzabile con i propri dati, costi di commissione.
from matplotlib import pyplot as plt
import numpy as np
def COMM(CAP,MIN,MAX,percent): # calcolo commissioni
ris=percent*CAP
if(ris<MIN):
ris=MIN
elif(ris>MAX):
ris=MAX
ris+=2.3 # 2.3 euro = spese di borsa, extra
return ris
MIN=7 #min = 7 euro
MAX=21 # max = 21 euro
percent=0.0015 # 0,15% spesa variabile fra MIN e MAX
plt.figure()
CAP=np.array([2500,5000,7500,10000,12500,15000])
for i in range(6):
plt.plot(CAP[i],0.5*(1+2*COMM(CAP[i],MIN,MAX,percent)/(CAP[i]*0.01)),'o',color='red') #delta = 1%
plt.plot(CAP[i],0.5*(1+2*COMM(CAP[i],MIN,MAX,percent)/(CAP[i]*0.02)),'o',color='green') #delta = 2%
plt.plot(CAP[i],0.5*(1+2*COMM(CAP[i],MIN,MAX,percent)/(CAP[i]*0.03)),'o',color='blue') #delta = 3%
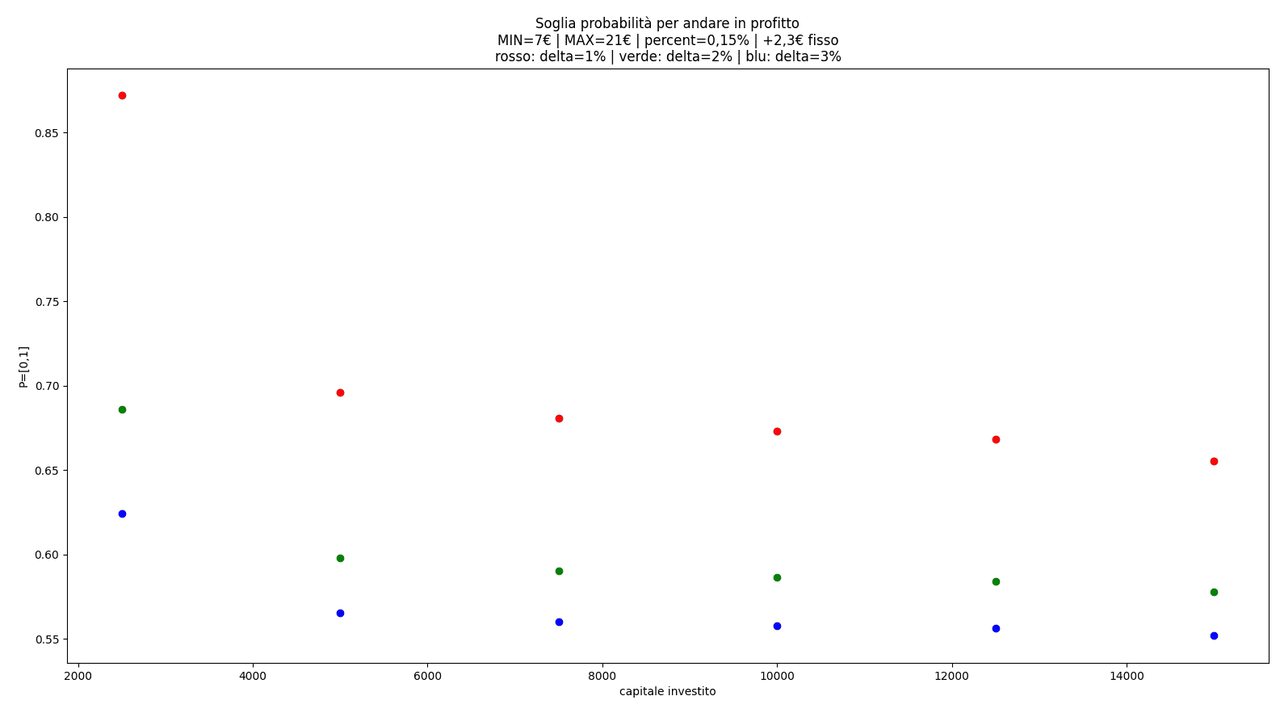
plt.title("Soglia probabilità per andare in profitto\nMIN=7€ | MAX=21€ | percent=0,15% | +2,3€ fisso\nrosso: delta=1% | verde: delta=2% | blu: delta=3%")
plt.xlabel("capitale investito")
plt.ylabel("P=[0,1]")
plt.show()
Vediamo ora i risultati di questo codice, mostrati in un grafico. I punti in blu (delta = ±3%) mostrano una maggiore convenienza probabilistica. Accettare una variazione più ampia (ricordiamo, nel bene e nel male, quindi lasciar correre la posizione in perdita significa aumentare il nostro rischio!) a parità di capitale investito e di condizioni (commissioni fisse e variabili), rende la soglia di probabilità più bassa (ovvero, per esempio, è sufficiente che la previsione sia accurata il 55% delle volte piuttosto che il 70%, chiaramente se il "peso" delle commissioni incide meno, finiamo per tendere asintoticamente al 50%).
